Mesa de sinuca e Números Complexos

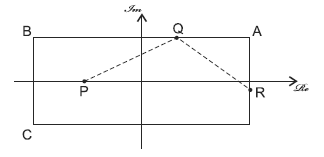
Os pontos A, B, C e D representam, no plano complexo, os vértices de uma mesa de
sinuca, retangular, de lados paralelos aos eixos coordenados e cujo centro O coincide
com a origem do referido sistema de coordenadas. Após uma tacada na direção de
z = 1 + i, uma bola colocada no ponto P segue até Q, na lateral dessa mesa, indo, em
seguida, até R.

Sabendo-se que a bola se desvia com o mesmo ângulo com que incide e que os pontos
A e P são afixos dos números complexos Z1 = 3 + 2i e Z2 = −1/2 , respectivamente,
pode-se afirmar que o ponto R é afixo de um número complexo cujo argumento principal
θ é tal que

01) 6tgθ = −1 (Gabarito)
02) 6tgθ = 1
03) 3tgθ = −2
04) 2tgθ = 3
05) 3tgθ = 4

EsdrasCFOPM escreveu:

A(3,2)
P(-1/2, 0)
Q(x, 2)
R(3, y)

A bola segue de P para Q e sabe-se que a reta PQ contém o complexo M(1, 1) (não representado), segundo o enunciado.
Com isso dá pra achar o ângulo QPT = a da figura: tga = Δy/Δx = (1 - 0)/(1 - (-1/2)) = 2/3.

A equação da reta PQ será, então: y - 1 = 2(x-1)/3 ----> y = (2x+1)/3 e encontra-se Q fazendo y = 2:
2 = (2x+1)/3 ----> x = 5/2 -----> Q(5/2, 2).

O enunciado diz que os ângulos PQT e RQT são iguais (incidência e reflexão). Logo, ΔPTQ é congruente a ΔSTQ pelo caso ALA ----> QST = a.

Agora dá pra achar R, pois temos as coordenadas de Q e o ângulo QST = a.
A equação da reta SQ será y - 2 = -2/3 (x - 5/2) ---> y = (11-2x)/3. Achamos a ordenada de R fazendo x = 3 ---> y = 5/3 ---> note que o ponto R deve acima do eixo real ----> R(3, 5/3) ----> tgθ = (5/3)/(3) = 5/9.

Seria incômodo você explicar o seu modo de resolver a um iniciante em matemática? Os termos e a explicação ficou complicada para mim.

O que você não entendeu? Tentou desenhar num papel o enunciado e depois fazer as anotações, no desenho, que eu falei na mensagem anterior?

1ª dúvida:

Por que A^QR = - θ?

2ª dúvida

Por que RQS = PQS = 90 - (-θ) ----> QPS = -θ, se R está diferente em relação a P. Como seriam iguais?

3ª Dúvida

De onde veio o T e por quê?

Esqueça a solução anterior pois eu calculei um ângulo que não era o argumento sem prestar atenção.
Agora eu editei a resolução, mas não encontrei nenhum gabarito. Leia-a e veja se encontra algum erro que permita ser arrumado a fim de encontrar a resposta. A princípio, não vi nenhum...

Esdras

Concordo com a solução do Ashitaka.

Evidentemente o desenho está totalmente fora de escala: o ponto P deveria ficar bem mais próximo da origem. Com isto o ponto R deveria ficar no 1º quadrante, bem próximo ao ponto A.

Tens certeza dos dados do enunciado? De onde você copiou? Podes postar uma imagem do enunciado original?

É uma questão da prova de Oficial da Polícia Militar da Bahia de 2014, mas quase ninguém faz a prova de matemática e erros passam despercebidos. Obrigado pela resolução Ashitaka!