Elipse - Raio vetor e normal
2 participantes
Página 1 de 1
Elipse - Raio vetor e normal
por gustavogc14 Sáb 21 Ago 2021, 16:57
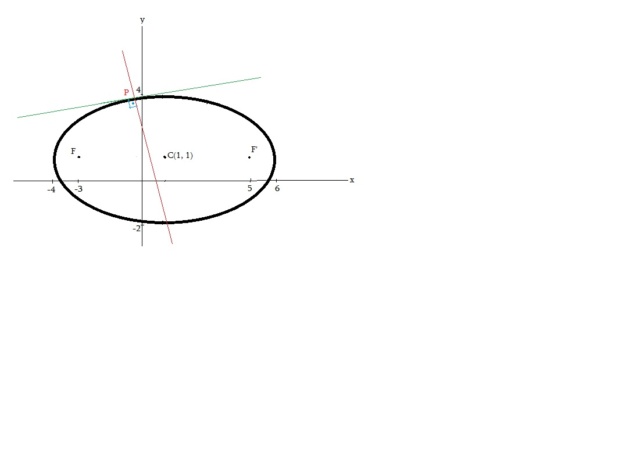
P é um ponto do 2º quadrante sobre a elipse E: [latex]\frac{(x-1)^2}{25}+\frac{(y-1)^2}{9}=1[/latex], extremo de um raio vetor medindo 2. A normal a E por P intersecta o eixo das abscissas em um ponto cuja soma das coordenadas é:
A) 8/5
B) -8/5
C) -7/5
D) 7/5
E) N.D.A.
A) 8/5
B) -8/5
C) -7/5
D) 7/5
E) N.D.A.
- Gabarito:
- A
gustavogc14- Padawan
- Mensagens : 61
Data de inscrição : 09/03/2021
Re: Elipse - Raio vetor e normal
por Elcioschin Sáb 21 Ago 2021, 18:25
Calcule y = f(x)
Calcule a derivada y' = f'(x)
f'(x) é o coeficiente angular m da reta tangente à curva no ponto P(xP, yP)
A reta normal à curva, no ponto P tem equação: y - yP = (-1/m).(x - xP)
(xP)² + (yP)² = 2²
Faça y = 0 e calcule x
Calcule a derivada y' = f'(x)
f'(x) é o coeficiente angular m da reta tangente à curva no ponto P(xP, yP)
A reta normal à curva, no ponto P tem equação: y - yP = (-1/m).(x - xP)
(xP)² + (yP)² = 2²
Faça y = 0 e calcule x
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
gustavogc14 gosta desta mensagem
Tópicos semelhantes» Tangente e Normal de uma elipse.
» Vetor normal a um plano
» Vetor normal a uma esfera
» Reta tangente e normal à elipse
» Geometria Analítica - Reta normal à elipse
» Vetor normal a um plano
» Vetor normal a uma esfera
» Reta tangente e normal à elipse
» Geometria Analítica - Reta normal à elipse
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
