W da Força Peso e Energia Potencial Gravitacional
2 participantes
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
 W da Força Peso e Energia Potencial Gravitacional
W da Força Peso e Energia Potencial Gravitacional
Galera, tô meio confuso em relação à interpretação do Trabalho da Força Peso e a Energia Potencial Gravitacional. Vou dizer o que eu entendi:
- O Trabalho da Força Peso na subida é Resistor (W<0) e na descida é Motor (W>0).
- Se eu jogo uma bola pra cima, a Energia Potencial Gravitacional da bola vai ser maior lá em cima do que na minha mão, certo?
É aí que eu não tô conseguindo interpretar o fenômeno: como essa Energia aumentou, sendo que o Trabalho é resistor na subida? Eu sei que a Epg é diretamente proporcional à altura. Mas o que faz a Energia Potencial Gravitacional ser maior lá em cima, de fato? E o contrário, quando a bola cai, o Trabalho é Motor, mas há uma perda de Energia Potencial Gravitacional, por que isso? Eu sei que a Epg vira Energia Cinética na descida, mas ainda tô travado com isso.
E eu sei que tá errado, mas se fosse pensar pela intuição, a Força peso daria energia pro corpo na descida, ou seja, o W seria Motor, e tiraria Energia na subida, ou seja, o W seria Resistor. Eu tô pensando como se fosse Energia Cinética, em que a a força peso desloca o objeto dando energia pra ele
Parece ser algo trivial, mas tô bugado, alguém me desbuga hahaha
- O Trabalho da Força Peso na subida é Resistor (W<0) e na descida é Motor (W>0).
- Se eu jogo uma bola pra cima, a Energia Potencial Gravitacional da bola vai ser maior lá em cima do que na minha mão, certo?
É aí que eu não tô conseguindo interpretar o fenômeno: como essa Energia aumentou, sendo que o Trabalho é resistor na subida? Eu sei que a Epg é diretamente proporcional à altura. Mas o que faz a Energia Potencial Gravitacional ser maior lá em cima, de fato? E o contrário, quando a bola cai, o Trabalho é Motor, mas há uma perda de Energia Potencial Gravitacional, por que isso? Eu sei que a Epg vira Energia Cinética na descida, mas ainda tô travado com isso.
E eu sei que tá errado, mas se fosse pensar pela intuição, a Força peso daria energia pro corpo na descida, ou seja, o W seria Motor, e tiraria Energia na subida, ou seja, o W seria Resistor. Eu tô pensando como se fosse Energia Cinética, em que a a força peso desloca o objeto dando energia pra ele
Parece ser algo trivial, mas tô bugado, alguém me desbuga hahaha
Última edição por Luís Miguel, o cantor em Sex 23 Abr 2021, 16:01, editado 1 vez(es)
Luís Miguel, o cantor- Iniciante
- Mensagens : 12
Data de inscrição : 25/01/2021
 Re: W da Força Peso e Energia Potencial Gravitacional
Re: W da Força Peso e Energia Potencial Gravitacional
não se esqueça que quando você joga algo para cima, você exerce uma força sobre esse algo.
Suponha que você jogou uma pedra para cima: a força que sua mão faz na pedra atua somente no momento de contato, esse força não realiza trabalho a partir do momento em que perde contado com sua mão, mas realiza trabalho quando você faz o movimento com o braço para lançar a pedra. Então, essa energia vem da energia química que você consome quando come alguma coisa, seu organismo transfere para pedra, a pedra recebe essa energia e entrega para o campo, pouco a pouco, no ponto mais alto toda energia fica armazenada no campo (que energia? A que VOCÊ forneceu para pedra ao lançar ela).
Fd-mgh=0 h=Fd/mgh, ou ainda, podemos considerar o fenômeno a partir do ponto em que ela sai da sua mão, você já entregou energia a ela, ela sai da sua mão com velocidade v: -mgh=-mv²/2 h=v²/2gh.
A outra pergunta: o que faz a energia potencial ser maior la em cima?
Para acabar com a ambiguidade considere o seguinte exemplo:
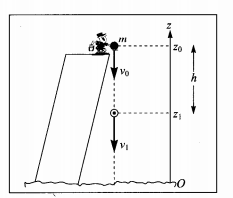
você provou, no curso de mecânica que v1²=v0²+2g(z0-z1)
multiplicando tudo por m/2 aqui: m/2v1²=m/2v0²+m/2(2gz0-2gz1)
fica assim:[latex]\frac{mv_1^2}{2}+mgz_1=\frac{mv_2^2}{2}+mgz_2[/latex]
note que, quando lançamos uma pedra no campo gravitacional, o termo mgz+mv²/2 se conserva, é tradição chamar mgz de potencial, e mv²/2 de cinética.
Portando no campo gravitacional, no referencial inercial [latex]E=\sum (\frac{1}{2}mv^2+mgz)[/latex] se conserva.
O que acontece se mudarmos de referencial, passando para outro, também inercial?
O que eu to querendo dizer com isso é que, em vez de considerar z=0 o chão, vamos considerar z=0 o ponto mais alto da trajetória da pedra e ver o que acontece:
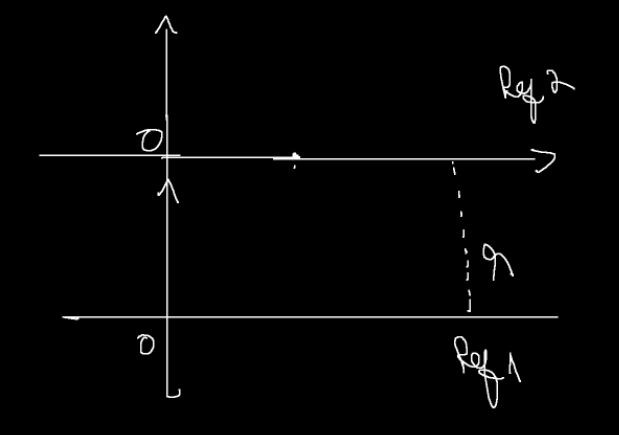
Passando do referencial 1 para o referencial dois as equações ficam assim:
ref 1: [latex]\frac{mv^2}{2}=mgh[/latex] utilizando o fator que se conserva como visto acima:
ref 2: [latex]\frac{mv^2}{2}-mgh=0[/latex]
viu que a energia potencial não depende de um ponto específico?
Quando encontramos o termo conservativo E ali em cima, usamos 2 pontos arbitrários e tomamos z=0 arbitrariamente.
Então, a energia potencial deve se conservar para TODO referencial inercial, ela independe do referencial, você pode escolher qualquer ponto arbitrário para chamar de origem, o movimento de um corpo em relação a essa origem deve respeitar a conservação, não existe uma origem privilegiada.
Suponha que você jogou uma pedra para cima: a força que sua mão faz na pedra atua somente no momento de contato, esse força não realiza trabalho a partir do momento em que perde contado com sua mão, mas realiza trabalho quando você faz o movimento com o braço para lançar a pedra. Então, essa energia vem da energia química que você consome quando come alguma coisa, seu organismo transfere para pedra, a pedra recebe essa energia e entrega para o campo, pouco a pouco, no ponto mais alto toda energia fica armazenada no campo (que energia? A que VOCÊ forneceu para pedra ao lançar ela).
Fd-mgh=0 h=Fd/mgh, ou ainda, podemos considerar o fenômeno a partir do ponto em que ela sai da sua mão, você já entregou energia a ela, ela sai da sua mão com velocidade v: -mgh=-mv²/2 h=v²/2gh.
A outra pergunta: o que faz a energia potencial ser maior la em cima?
Para acabar com a ambiguidade considere o seguinte exemplo:

você provou, no curso de mecânica que v1²=v0²+2g(z0-z1)
multiplicando tudo por m/2 aqui: m/2v1²=m/2v0²+m/2(2gz0-2gz1)
fica assim:[latex]\frac{mv_1^2}{2}+mgz_1=\frac{mv_2^2}{2}+mgz_2[/latex]
note que, quando lançamos uma pedra no campo gravitacional, o termo mgz+mv²/2 se conserva, é tradição chamar mgz de potencial, e mv²/2 de cinética.
Portando no campo gravitacional, no referencial inercial [latex]E=\sum (\frac{1}{2}mv^2+mgz)[/latex] se conserva.
O que acontece se mudarmos de referencial, passando para outro, também inercial?
O que eu to querendo dizer com isso é que, em vez de considerar z=0 o chão, vamos considerar z=0 o ponto mais alto da trajetória da pedra e ver o que acontece:

Passando do referencial 1 para o referencial dois as equações ficam assim:
ref 1: [latex]\frac{mv^2}{2}=mgh[/latex] utilizando o fator que se conserva como visto acima:
ref 2: [latex]\frac{mv^2}{2}-mgh=0[/latex]
viu que a energia potencial não depende de um ponto específico?
Quando encontramos o termo conservativo E ali em cima, usamos 2 pontos arbitrários e tomamos z=0 arbitrariamente.
Então, a energia potencial deve se conservar para TODO referencial inercial, ela independe do referencial, você pode escolher qualquer ponto arbitrário para chamar de origem, o movimento de um corpo em relação a essa origem deve respeitar a conservação, não existe uma origem privilegiada.
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor

- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
 Re: W da Força Peso e Energia Potencial Gravitacional
Re: W da Força Peso e Energia Potencial Gravitacional
Existe uma tendência que parece ser universal, que tudo procura a mínima energia potencial, um elétron, uma molécula, existem diversas leis baseadas nisso.
Quando você adota z=0 arbitrariamente como o referencial para o campo gravitacional, qualquer coisa acima dessa linha tem energia potencial maior que em z=0, portanto qualquer corpo (com massa é claro), que esteja na presença exclusiva desse campo, tende a voltar para z=0.
valores negativos de z possuem potencial menor, então, se for possível descer mais, o corpo tende a ir ainda mais para baixo, a menor energia potencial possível seria no núcleo do planeta. Se não existisse superfície terrestre, os corpos cairiam em direção ao núcleo, ao chegar no núcleo, por possuirem velocidade, começariam a subir em direção ao hemisfério oposto, com a velocidade diminuindo sempre, até voltar a mesma altura que foi solta inicialmente, e esse movimento se repete com um período bem definido, trata-se de um MHS.
A energia potencial de um mhs é característica, próximo de uma parábola com concavidade voltado para baixo, logo possui mínimo no centro da Terra, mas como não é possível cair até o núcleo, os corpos seguem um pequeno trecho da curva de potencial até serem interrompidos.
Quando você adota z=0 arbitrariamente como o referencial para o campo gravitacional, qualquer coisa acima dessa linha tem energia potencial maior que em z=0, portanto qualquer corpo (com massa é claro), que esteja na presença exclusiva desse campo, tende a voltar para z=0.
valores negativos de z possuem potencial menor, então, se for possível descer mais, o corpo tende a ir ainda mais para baixo, a menor energia potencial possível seria no núcleo do planeta. Se não existisse superfície terrestre, os corpos cairiam em direção ao núcleo, ao chegar no núcleo, por possuirem velocidade, começariam a subir em direção ao hemisfério oposto, com a velocidade diminuindo sempre, até voltar a mesma altura que foi solta inicialmente, e esse movimento se repete com um período bem definido, trata-se de um MHS.
A energia potencial de um mhs é característica, próximo de uma parábola com concavidade voltado para baixo, logo possui mínimo no centro da Terra, mas como não é possível cair até o núcleo, os corpos seguem um pequeno trecho da curva de potencial até serem interrompidos.
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor

- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
 Re: W da Força Peso e Energia Potencial Gravitacional
Re: W da Força Peso e Energia Potencial Gravitacional
Caramba, genial! Agora entendi. Brigadão pela aula, monstro sagrado!
Luís Miguel, o cantor- Iniciante
- Mensagens : 12
Data de inscrição : 25/01/2021
 Re: W da Força Peso e Energia Potencial Gravitacional
Re: W da Força Peso e Energia Potencial Gravitacional
Luís Miguel, o cantor escreveu:Caramba, genial! Agora entendi. Brigadão pela aula, monstro sagrado!
De nada amigo, que bom que ajudou.
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor

- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
 Tópicos semelhantes
Tópicos semelhantes» Força gravitacional/Energia Potencial Gravitacional
» Força Peso x Força Gravitacional
» Força Gravitacional- Força-Peso
» Força Peso e Força Gravitacional
» MCU - Força Peso > Força Normal
» Força Peso x Força Gravitacional
» Força Gravitacional- Força-Peso
» Força Peso e Força Gravitacional
» MCU - Força Peso > Força Normal
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












