Equação Matricial

Boa tarde !  A equação matricial do exercício :

[latex]\begin{bmatrix} cos A & seno A \\ -seno A & cos A \end{bmatrix} * X = \begin{bmatrix} cos 2A\\ sen 2A \end{bmatrix} [/latex]


Consegui chegar até :

[latex]\begin{bmatrix} cos A & seno A \\ -seno A & cos A \end{bmatrix} * \begin{bmatrix} Z\\ Y \end{bmatrix} = \begin{bmatrix} cos 2A\\ sen 2A \end{bmatrix}[/latex]


[latex]\left\{\begin{matrix} cos A * Z + sen A * Y = cos 2A \\ - sen A * Z + cos A * Y = sen 2A \end{matrix}\right. [/latex]


[latex] Y = \frac{cos 2A- cos A*Z}{sen A} [/latex]


[latex] Z = \frac{sen 2A- cos A* Y}{- sen A} [/latex]



Depois fiquei na dúvida, não estou conseguindo continuar...



O gabarito é :

[latex] X = \begin{bmatrix} cos 3A\\ sen 3A \end{bmatrix} [/latex]

Em



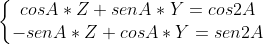
Multiplique a 1ª equação por sen A e a 2ª Equação por cos A. Dessa forma,teremos:


Y(sen²A + cos²A) = cos2AsenA + sen2AcosA

Como sen²A + cos²A = 1,e o 2º membro representa uma soma de arcos,obtem-se:

Y = sen3A

Para Z,multiplicaremos a 1ª equação por cosA e a 2ª por - senA. Assim,tem-se:

Z(cos²A + sen²A) = cos2AcosA - sen2AsenA

semelhante ao 1º processo,o 2º membro é uma soma de arcos cosseno.

Z = cos3A

Pode me explicar como você fez a multiplicação das equações ? Por favor...

Você não pode ter dúvidas:

Multiplique a 1ª equação por senA --> Ensino Fundamental
Multiplique a 2º equação por cosA --> Ensino Fundamental

Some as duas equações obtidas --> --> Ensino Fundamental

Vc obterá Y = cos(2.A).senA + cosA.sen(2.a) = sen(3.A) --> Ensino Médio

Não posso mas estava com dúvidas...


Estava tentando calcular e achando que algo mais deveria ser feito, mas consegui chegar ao resultado depois de algumas tentativas.

Pensei que poderia tirar minhas dúvidas aqui tranquilamente, mas visivelmente não posso...

Beatrix Ferreira escreveu:Pode me explicar como você fez a multiplicação das equações ? Por favor...

Beatriz,creio que tenha sido erro meu,não fui muito claro com a minha resolução.

Multipliquei a 1ª equação por sen A e a 2ª por cos A obtendo:

(sen Acos A)Z + (sen²A)Y = cos 2AsenA
-(cos AsenA)Z + (cos²A)Y = sen 2AcosA

Feito isso,SOMEI as duas equações e obtive um expressão somente em função de Y. Pela relação fundamental,sen²A + cos²A = 1,logo:

(sen²A + cos²A)Y = cos 2AsenA + sen2AcosA

O 2º membro é equivalente a uma soma de arcos sen(A + 2A)

Y = sen 3A

Tinha esquecido de mencionar o fato de que havia somado as duas equações após multiplicá-las.

OBS: Como se trata se um sistema 2x2,e usar substituição acaba não facilitando a resolução,creio que a resolução por Cramer possa ser mais didática.