Coordenadas Cilíndricas
2 participantes
Página 1 de 1
 Coordenadas Cilíndricas
Coordenadas Cilíndricas
Calcule 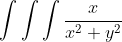 onde E é a região do primeiro octante interna ao cilindro x²+y²-2y=0, externa ao cilindro x²+y²=1, abaixo do paraboloide z=9-x²-y² e acima do paraboloide z=1+x²+y²
onde E é a região do primeiro octante interna ao cilindro x²+y²-2y=0, externa ao cilindro x²+y²=1, abaixo do paraboloide z=9-x²-y² e acima do paraboloide z=1+x²+y²
Alguém???
Resp: 13/12
Alguém???
Resp: 13/12
Gabs lopes- Iniciante
- Mensagens : 2
Data de inscrição : 19/09/2020
Idade : 28
Localização : Santa Luzia, MG, Brasil
 Re: Coordenadas Cilíndricas
Re: Coordenadas Cilíndricas
Olá Gabs lopes! 
Antes de começarmos a fazer as contas, é sempre bom termos um esboço da figura para nos auxiliar. Veja:

Agora a ideia clássica é substituir x = r.cosθ e y = r.senθ para encontrar as relações entre r, θ e z. Antes disso, no entanto, vamos encontrar os limites dos valores que θ pode assumir. Veja que os cilindros definem θ, e que podemos analisar θ sobre o plano xy:
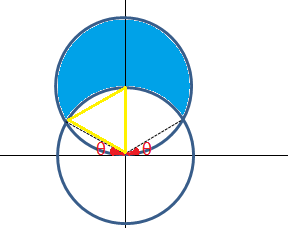
Perceba que o triângulo amarelo é equilátero, de lado 1. Sendo assim, como a região delimitada no enunciado pode assumir os valores de x e y dos pontos pertencentes à região hachurada, e como a região é limitada ao primeiro octante, teremos que 30° < θ < 90°. Agora vamos limitar r e z, veja:
[latex]\\\bullet\left\{\begin{matrix}x^2+y^2> 1\\ x^2+y^2< 2y\end{matrix}\right.\;\rightarrow\;\left\{\begin{matrix}r^2> 1\\ r^2< 2r\sin\theta\end{matrix}\right.\;\rightarrow\;1 < r < 2\sin\theta [/latex]
[latex]\\\bullet\left\{\begin{matrix}z> 1+x^2+y^2\\ z< 9-x^2-y^2\end{matrix}\right.\;\rightarrow\;1+r^2 < z < 9-r^2[/latex]
Agora que já temos os limites das nossas variáveis, temos que aplicar a seguinte ideia na integral tripla:
[latex]\\\int \int \int f(x,y,z).dV= \int \int \int f(r\cos\theta,r\sin\theta,z).r.dz.dr.d\theta[/latex]
Aplicando esta ideia, e colocando como os limites de integração os limites encontrados para cada variável, teremos:
[latex]\\\int \int \int \frac{x}{x^2+y^2}.dV= \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \int_{1}^{2\sin\theta}\int_{1+r^2}^{9-r^2} \frac{r\cos\theta}{r^2}.r.dz.dr.d\theta\\\\ =\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos\theta.d\theta \int_{1}^{2\sin\theta}dr\int_{1+r^2}^{9-r^2} .dz\\\\ =\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos\theta.d\theta \int_{1}^{2\sin\theta}(8-2r^2)dr\\\\ =\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos\theta.(16\sin\theta-\frac{16\sin^3\theta}{3}-\frac{22}{3}).d\theta\\\\ =\frac{13}{12} [/latex]
Antes de começarmos a fazer as contas, é sempre bom termos um esboço da figura para nos auxiliar. Veja:

Agora a ideia clássica é substituir x = r.cosθ e y = r.senθ para encontrar as relações entre r, θ e z. Antes disso, no entanto, vamos encontrar os limites dos valores que θ pode assumir. Veja que os cilindros definem θ, e que podemos analisar θ sobre o plano xy:

Perceba que o triângulo amarelo é equilátero, de lado 1. Sendo assim, como a região delimitada no enunciado pode assumir os valores de x e y dos pontos pertencentes à região hachurada, e como a região é limitada ao primeiro octante, teremos que 30° < θ < 90°. Agora vamos limitar r e z, veja:
[latex]\\\bullet\left\{\begin{matrix}x^2+y^2> 1\\ x^2+y^2< 2y\end{matrix}\right.\;\rightarrow\;\left\{\begin{matrix}r^2> 1\\ r^2< 2r\sin\theta\end{matrix}\right.\;\rightarrow\;1 < r < 2\sin\theta [/latex]
[latex]\\\bullet\left\{\begin{matrix}z> 1+x^2+y^2\\ z< 9-x^2-y^2\end{matrix}\right.\;\rightarrow\;1+r^2 < z < 9-r^2[/latex]
Agora que já temos os limites das nossas variáveis, temos que aplicar a seguinte ideia na integral tripla:
[latex]\\\int \int \int f(x,y,z).dV= \int \int \int f(r\cos\theta,r\sin\theta,z).r.dz.dr.d\theta[/latex]
Aplicando esta ideia, e colocando como os limites de integração os limites encontrados para cada variável, teremos:
[latex]\\\int \int \int \frac{x}{x^2+y^2}.dV= \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \int_{1}^{2\sin\theta}\int_{1+r^2}^{9-r^2} \frac{r\cos\theta}{r^2}.r.dz.dr.d\theta\\\\ =\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos\theta.d\theta \int_{1}^{2\sin\theta}dr\int_{1+r^2}^{9-r^2} .dz\\\\ =\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos\theta.d\theta \int_{1}^{2\sin\theta}(8-2r^2)dr\\\\ =\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\cos\theta.(16\sin\theta-\frac{16\sin^3\theta}{3}-\frac{22}{3}).d\theta\\\\ =\frac{13}{12} [/latex]

Victor011- Fera

- Mensagens : 663
Data de inscrição : 21/10/2015
Idade : 26
Localização : Rio de Janeiro, Brasil
Gabs lopes gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Coordenadas Cilíndricas - Integral Tripla
» Coordenadas cilíndricas e esféricas
» Coordenadas Cilíndricas - Integral Tripla
» Transforme para coordenadas cilíndricas
» Integral tripla em coordenadas cilíndricas
» Coordenadas cilíndricas e esféricas
» Coordenadas Cilíndricas - Integral Tripla
» Transforme para coordenadas cilíndricas
» Integral tripla em coordenadas cilíndricas
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












