Geometria Plana

por Bruna Ce Ter 15 Set 2020, 14:06

Determine a medida x+y, sendo ABCDE um pentágono regular e DEF um triângulo equilátero.

Desculpe que não tenho o gabarito, estou tentando encontrar.

por **Christian M. Martins** Ter 15 Set 2020, 14:45

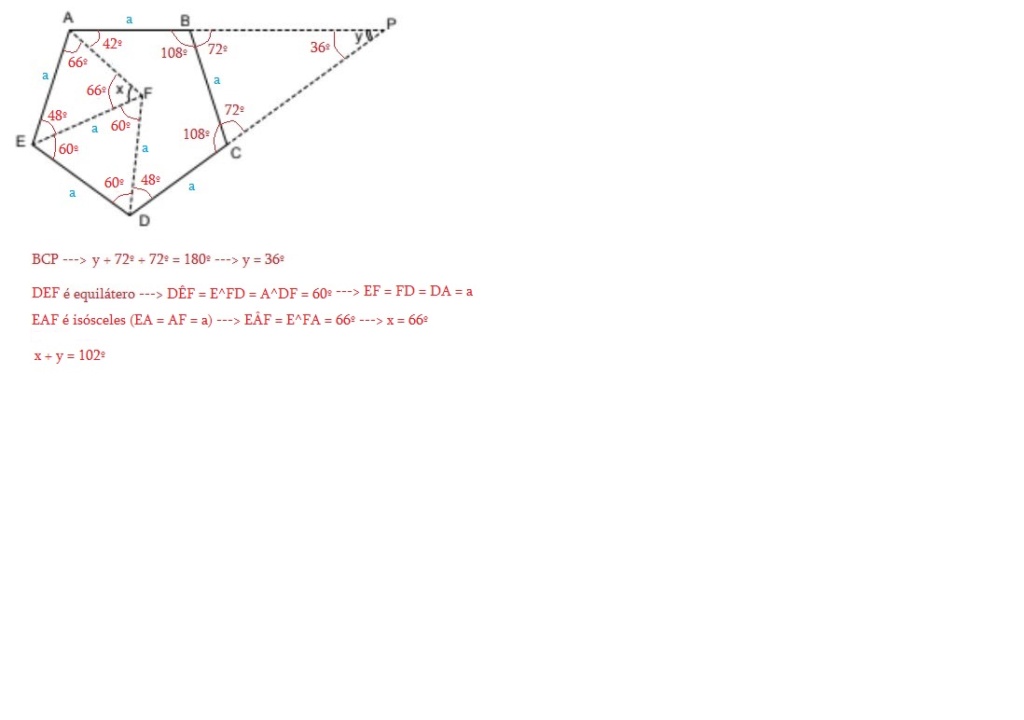
ABCDE é regular e DEF é equilátero, então AÊF = AÊD - FÊD = 108 - 60 = 48°
AEF é isósceles, sendo os ângulos EÂF = A^FE = x = (180 - AÊF)/2 = (180 - 48)/2 = 66°
x = 66°

BCP é isósceles, sendo os ângulos B^CP = C^BP = 180 - 108 = 72°. Logo, y = 180 - (B^CP + C^BP) = 180 - (72*2) = 36°
y = 36°

x + y = 66 + 36 = 102°

por **Elcioschin** Ter 15 Set 2020, 18:06

Uma figura para entender a solução do Christian:

por **Christian M. Martins** Ter 15 Set 2020, 18:17

Por que AEF é equilátero? AÊD = 108° (já que ABCDE é um pentágono regular), DÊF = 60° (já que DEF é triângulo equilátero), então AÊF = AÊD - DÊF = 48°. Como AEF tem dois lados congruentes e um ângulo de 48°, se conclui que é isósceles, sendo os outros dois ângulos iguais a (180 - AÊF)/2 = (180 - 48)/2 = 132/2 = 66°.