integral tripla
2 participantes
Página 1 de 1
integral tripla
por Omagodasexatas3,14 Sáb 20 Jun 2020, 12:59
Calcule 
onde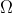 
= {(x,y,z)
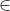R^3 | x>0,y>0,z>0} e 'a' é um número real diferente de 0 .
Obs:Não tenho a resposta. Mas cheguei no seguinte resultado: (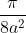
). Gostaria de saber se está correto.
Obs:Não tenho a resposta. Mas cheguei no seguinte resultado: (
Omagodasexatas3,14- Recebeu o sabre de luz
- Mensagens : 111
Data de inscrição : 07/09/2017
Idade : 28
Localização : São Paulo, São paulo, Brasil
Re: integral tripla
por JoaoGabriel Dom 21 Jun 2020, 09:15
Omega --> região de integração
e^(-a²*(x²+y²+z²)) = e^(-a²*x²)*e^(-a²*y²)*e^(-a²*z²)
Integrando em relação a x:
z*e^(-a²*x²)*e^(-a²*y²)*e^(-a²*z²) --> z*e^(-a²*y²)*e^(-a²*z²) = cte.
Integral de 0 a +inf de e^(-a²*x²) = sqrt(pi)/a^2 --> integral Gaussiana
Em Y teremos a mesma situação:
Integral de 0 a +inf de e^(-a²*y²) = sqrt(pi)/a^2 --> integral Gaussiana
Para Z, teremos integração por partes:
Integral de 0 a +inf de z*e^(-a²*z²) = 1/8
Portanto teremos (1/
* sqrt(pi)/a^2 * sqrt(pi)/a^2 = pi/(8*a^4)
e^(-a²*(x²+y²+z²)) = e^(-a²*x²)*e^(-a²*y²)*e^(-a²*z²)
Integrando em relação a x:
z*e^(-a²*x²)*e^(-a²*y²)*e^(-a²*z²) --> z*e^(-a²*y²)*e^(-a²*z²) = cte.
Integral de 0 a +inf de e^(-a²*x²) = sqrt(pi)/a^2 --> integral Gaussiana
Em Y teremos a mesma situação:
Integral de 0 a +inf de e^(-a²*y²) = sqrt(pi)/a^2 --> integral Gaussiana
Para Z, teremos integração por partes:
Integral de 0 a +inf de z*e^(-a²*z²) = 1/8
Portanto teremos (1/
* sqrt(pi)/a^2 * sqrt(pi)/a^2 = pi/(8*a^4)
JoaoGabriel- Monitor
- Mensagens : 2344
Data de inscrição : 30/09/2010
Idade : 29
Localização : Rio de Janeiro
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
