Cáculo 2 , Integrais Duplas

O centro de massa de de uma região plana D de 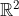, de densidade homogênea, é o ponto de coordenadas dadas por :

  e   

Onde A é a área da região D.
Com base nas informações acima, calcule as coordenadas do centro de massa da metade superior (y>0) da região delimitada pela elipse:


Obs: Não tenho a resposta, estou com dificuldades para resolver este exrecício, se alguém puder me ajudar a resolve-lo, agradeço.

Equação da Elipse: x²/a² + y²/b² = 1 --> comparando com sua equação: a = 2 e b = 3

A área da elipse é dada por A = pi*a*b (demonstre!), portante:

A = pi*2*3 = 6*pi

A parte superior da área limitada pela elipse está compreendida, em termos de x, de -a até a, ou seja, de -2 até 2.

x²/4 + y²/9 = 1 (x36)

9x² + 4y² = 36 --> 4y² = 36 - 9x² --> y = +- (1/2)*sqrt(36 - 9x²) 

y = +- (3/2)*sqrt(4-x²)

Em termos de y, a parte superior está compreendida de y = 0 até 
y = + (3/2)*sqrt(4-x²). Assim, o centro de massa pode ser calculado:

x_CM = (1/6*pi) * int(-2,2) x dx * int(0,+ (3/2)*sqrt(4-x²) ) dy = 0 --> Pela própria simetria da figura, sabemos que o x_CM deveria ser em zero.

y_CM --> faça o mesmo cálculo

JoaoGabriel escreveu:Equação da Elipse: x²/a² + y²/b² = 1 --> comparando com sua equação: a = 2 e b = 3

A área da elipse é dada por A = pi*a*b (demonstre!), portante:

A = pi*2*3 = 6*pi

A parte superior da área limitada pela elipse está compreendida, em termos de x, de -a até a, ou seja, de -2 até 2.

x²/4 + y²/9 = 1 (x36)

9x² + 4y² = 36 --> 4y² = 36 - 9x² --> y = +- (1/2)*sqrt(36 - 9x²) 

y = +- (3/2)*sqrt(4-x²)

Em termos de y, a parte superior está compreendida de y = 0 até 
y = + (3/2)*sqrt(4-x²). Assim, o centro de massa pode ser calculado:

x_CM = (1/6*pi) * int(-2,2) x dx * int(0,+ (3/2)*sqrt(4-x²) ) dy = 0 --> Pela própria simetria da figura, sabemos que o x_CM deveria ser em zero.

y_CM --> faça o mesmo cálculo

     Olá João gabriel, só pra saber se eu entendi então. No caso de y_CM será o mesmo cálculo feito pra o x_CM, só que vai ser a integral dupla de ydA  certo ? Ai o centro de massa de y será 2/pi.  Logo o centro de massa da parte superior da elipse (y>0) será (0,(2/pi)) certo ?

Perfeito, amigo! É exatamente esse o resultado. Complementando:

Muito obrigado !!!
Só mais uma pergunta se me permitir, me surgiu uma dúvida. Por que  devemos calcular a área completa da elipse(na integral dupla) se queremos encontrar apenas o centro de massa da parte superior da elipse ?
att,
Omago

Você tem toda razão. A área correta é (1/2)*pi*a*b, que vai dar 3*pi, de modo que a resposta final será (0, 4/pi).

Descuido meu.

JoaoGabriel escreveu:Você tem toda razão. A área correta é (1/2)*pi*a*b, que vai dar 3*pi, de modo que a resposta final será (0, 1/pi).

Descuido meu.

Na verdade o Y_CM será 4/pi, pois como o denominador é dividido por 2 (1/(A/2), o resultado final irá dobrar, sendo (2/pi)*2 = 4/pi.
Mas mesmo assim muito obrigado, me ajudou a resolver !