Geometria Plana

por Bruna Ce Sáb 23 maio 2020, 16:06

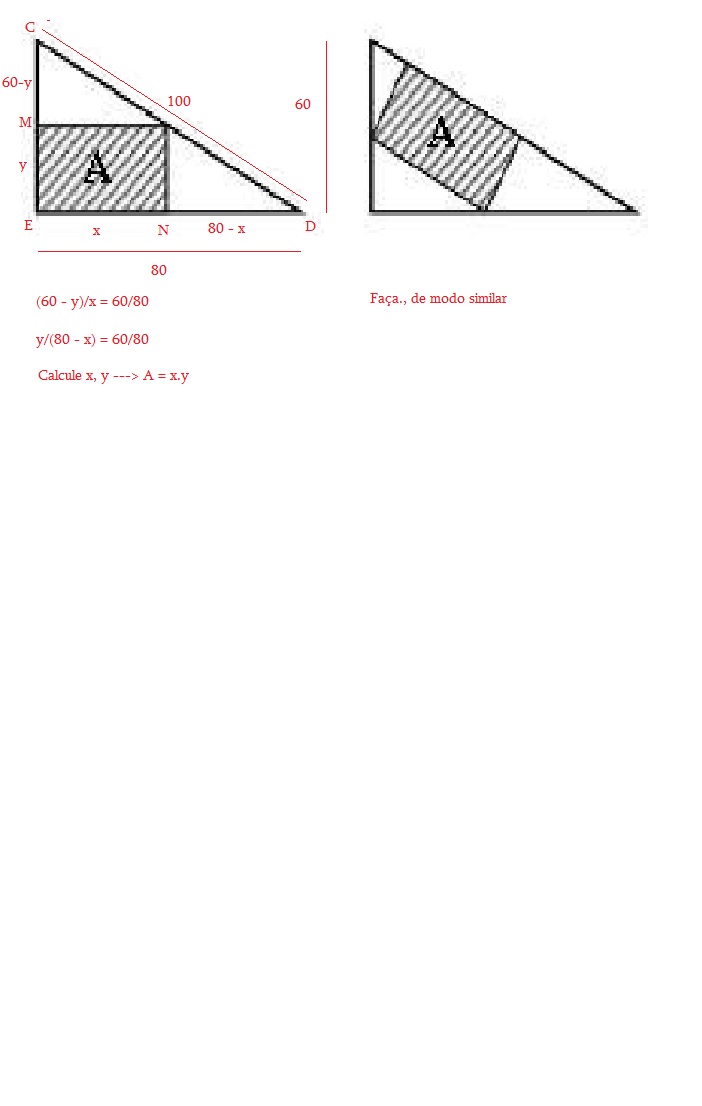
Numa vidraçaria há um pedaço de espelho sob a forma de um triângulo retângulo com os lados medindo 60 cm, 80 cm e 1 m. Quer-se, a partir dele, recortar um pedaço de espelho retangular com a maior área possível. A fim de economizar corte, pelo menos um dos lados do retângulo deve estar sobre um lado do triângulo.

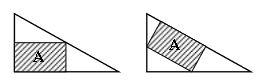
As posições sugeridas são as das figuras acima. Com base nessas informações, é certo afirmar que:

A) A1= A2
B) A1= (3/4)A2
C) A1= (4/3)A2
D) A1= (1/3)A2
E) A1= (9/16)A2

Correta alternativa A.

por **Elcioschin** Sáb 23 maio 2020, 16:30

por Bruna Ce Sáb 23 maio 2020, 16:55

Não consegui =/ Estou quando substituo as equações encontro y = 0

por **Elcioschin** Sáb 23 maio 2020, 17:31

60 - y ....... y
------- = --------
... x ...... 80 - x

x.y = (60 - y.).(80 - x) ---> x.y = 4800 - 60.x - 80.y + x.y

60.x + 80.y = 4800 ---> 3.x + 4.y = 240 ---> y = 60 - 3.x/4

Área ---> S(A) = x.y ---> S(A) = x.(60 - 3.x/4) ---> S(A) = - (3/4).x² + 60.x

A função é uma parábola com a concavidade voltada para cima: o valor máximo ocorre no vértice:

xV = - 60/2.(-3/4) ---> xV = 40 cm

y = 60 - (3/4).x ---> 60 - (3/4).40 ---> y = 30 cm

S(A) = 40.30 ---> S(A) = 1 200 cm²

por Bruna Ce Sáb 23 maio 2020, 17:49

Obrigada!! Poderia montar o esquema na imagem segunda figura? Não estou conseguido, tenho muitas dificuldades. Só indicando as medidas já é o suficiente.

por **Elcioschin** Sáb 23 maio 2020, 18:13

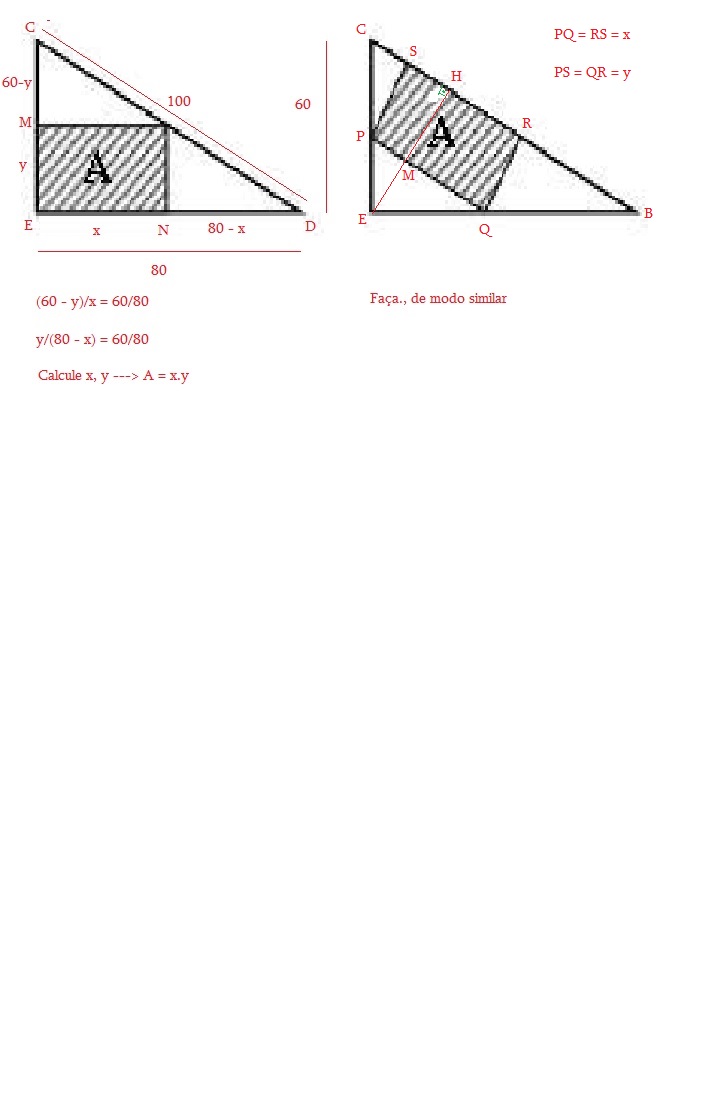
Chame de x a base do retângulo (na hipotenusa) e dentro do triângulo e y as alturas
Trace a altura EH referente à base CD. Calcule EH
Seja a base PQ do retângulo quem tem vértices sobre os catetos do triângulo e seja RS a mesma base x sobre a hipotenusa. Seja PS = QR = y
Seja M o ponto de encontro EH com PQ: MH = y ---> EM = EH - y

Agora faça semelhança dos triângulos EPQ com EBC e complete

por Bruna Ce Dom 24 maio 2020, 15:44

Não entendi onde estão o ponto M e N

por **Elcioschin** Dom 24 maio 2020, 19:35

Eu errei na digitação:

Considere a base PQ do retângulo, dentro do triângulo, sendo P o vértice do retângulo sobre o cateto menor e Q sobre o cateto maior do triângulo EBC

M é o ponto de encontro de EH com PQ

A semelhança deve ser feita entre os triângulos EPQ e EBC

por Bruna Ce Dom 24 maio 2020, 20:30

Agora consegui!! Muito obrigada mesmo!!

por **Elcioschin** Seg 25 maio 2020, 10:50

Então mostre o passo-a-passo da sua solução para que outros usuários aprendam com ela.

Melhorei a explicação nas mensagens anteriores; vou anexar um desenho para você usar: