Geometria Analítica, retas e plano cartesiano.

por Felipemlvr Sáb 04 Abr 2020, 22:41

Ao desenhar o logotipo de uma empresa automotiva, um designer verificou que dois lados de um paralelogramo estão contidos nas retas y = 3x e 2x + y = 0. Um terceiro lado poderia estar contido na reta:

a) y - 3x = 0
b) y = -2x
c) y = ½x
d) y = ⅓x
e) y = -2x + 4

Não possuo a resposta. Desde já agradeço a quem puder ajudar.

por marcelindo3301 Sáb 04 Abr 2020, 22:53

Se duas retas são paralelas os coeficientes angulares delas são iguais.

y=ax+b, o 'a' é o coeficiente angular.

Para formar um paralelogramo basta os lados opostos dele serem paralelos, ou seja, fazerem o mesmo ângulo com uma reta horizontal.

O coeficiente angular da reta y = 3x é 3 e o coeficiente angular da reta 2x + y = 0 é -2 (o exercício faz uma pegadinha aqui, você tem que "passar para o outro lado" o 2x, ficando y=-2x, sendo mais fácil de visualizar o coeficiente angular).

Agora basta olhar nas alternativas qual delas tem o mesmo coeficiente angular de alguma das duas retas dadas (3 ou -2).

a) y - 3x = 0 --> falsa, é a mesma reta dada no enunciado (y=3x).
b) y = -2x --> falsa, mesma reta dada no enunciado (2x+y=0)
c) y = ½x -- > falsa, coeficiente angular é 1/2.
d) y = ⅓x --> falsa, coeficiente angular é 1/3
e) y = -2x + 4 --> verdadeira, coeficiente angular igual a -2, igual o coeficiente angular da reta y=-2x.

Portanto, resposta letra "e".

por **Elcioschin** Dom 05 Abr 2020, 01:03

Um outro modo, mais completo, que vai ajudar a descobrir um erro do gabarito:

y = 3.x ---> Esta reta passa por A(1, 3)

y = - 2.x ---> Esta reta passa por C(1, -2)

O ponto comum às duas é B(0, 0)

1) Equação da reta CD, paralela à reta AB:

y - yB = 3.(x - xB) ---> y - (-2) = 3.(x - 1) ---> y = 3.x - 1

Esta reta não consta nas alternativas

2) Equação da reta do lado AD, paralela à reta BC:

y - yA = - 2.(x - xA) ---> y - 3 = - 2.(x - 1) ---> y = - 2.x + 5

Só pode ser alternativa E mas o termo independente é 5 (e não 4)

por marcelindo3301 Dom 05 Abr 2020, 10:58

Élcio, não entendi o motivo das retas terem que passar pelos pontos (1, 3) e (1, -2), achei que o único pré-requisito era ser paralela a alguma das retas dadas.

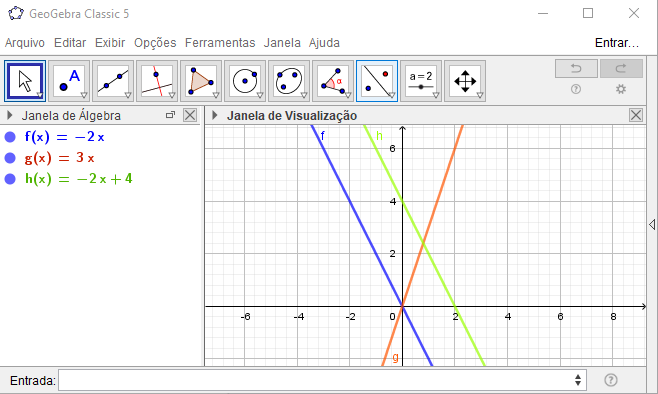
Geometria Analítica, retas e plano cartesiano. Screen65

Por que a reta y=-2x + 4 está errada? Se eu pegar qualquer outra reta que existe e que tem o coeficiente angular igual a 3 e o termo independente diferente de 0 o paralelogramo estaria formado.

por **Elcioschin** Dom 05 Abr 2020, 11:14

Marcelindo

Você está coberto de razão!!!
Quando eu escolhi os pontos A(1, 3) e C(1, -2), eu assumi, erradamente, que estes eram os vértices do paralelogramo.
Nesta questão NÃO dá para calcular os vértices porque não foram dados os valores dos lados do paralelogramo.

E o mais importante NÃO dá para calcular a equação correta de uma das retas que contém os outros dois lados. O enunciado pede :

Um terceiro lado poderia estar contido na reta:

Assim, o máximo que se pode calcular é o coeficiente angular das duas retas e procurar nas alternativas, qual delas poderia ser uma das retas pedidas

E foi exatamente o que você fez!