Inequações-produto
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Inequações-produto
por FernandoFRN Sex 27 Mar 2020, 09:24
Fundamentos de matemática elementar 1 edição de 2013
218. Resolva, em ℝ, as inequações:
a) (5x + 4)⁴ . (7x - 2)³ ≥ 0
Resposta do livro: S = {x∈ℝ | x ≥ 2/7}
Imagem da minha resolução da questão.
A minha dúvida é a seguinte: Se o ponto 2/7 foi incluído como ponto igual a 0, por que -4/5 não foi?
218. Resolva, em ℝ, as inequações:
a) (5x + 4)⁴ . (7x - 2)³ ≥ 0
Resposta do livro: S = {x∈ℝ | x ≥ 2/7}
Imagem da minha resolução da questão.A minha dúvida é a seguinte: Se o ponto 2/7 foi incluído como ponto igual a 0, por que -4/5 não foi?
Última edição por FernandoFRN em Sex 27 Mar 2020, 13:31, editado 8 vez(es)
FernandoFRN- Iniciante
- Mensagens : 11
Data de inscrição : 03/07/2019
Idade : 22
Localização : Belém-PA
Re: Inequações-produto
por lejandrocohen Sex 27 Mar 2020, 09:37
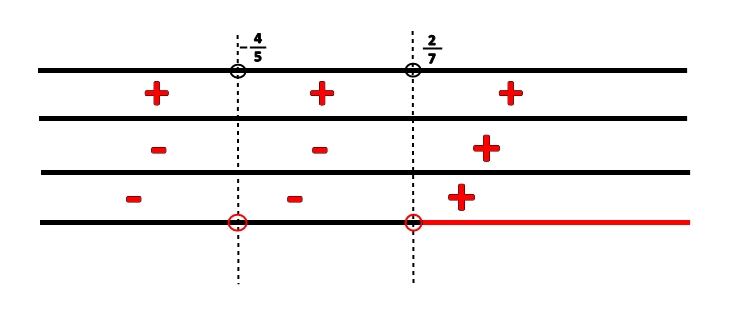
Pois ele quer que a inequação produto seja positiva (maior ou igual),e se você substituir para tirar a prova real,verá que ela só será positiva se x≥2/7, para valores abaixo de 2/7 ela será negativa,o que não se pede
lejandrocohen- Padawan
- Mensagens : 54
Data de inscrição : 08/07/2019
Idade : 25
Localização : Natal-RN
Re: Inequações-produto
por FernandoFRN Sex 27 Mar 2020, 09:57
Ignore ESTA mensagem.
Última edição por FernandoFRN em Sex 27 Mar 2020, 10:15, editado 1 vez(es)
FernandoFRN- Iniciante
- Mensagens : 11
Data de inscrição : 03/07/2019
Idade : 22
Localização : Belém-PA
Re: Inequações-produto
por FernandoFRN Sex 27 Mar 2020, 10:14
Eu tinha pensado a mesma coisa, mas o item c) da mesma questão me deixou em dúvida.lejandrocohen escreveu:Pois ele quer que a inequação produto seja positiva (maior ou igual),e se você substituir para tirar a prova real,verá que ela só será positiva se x≥2/7, para valores abaixo de 2/7 ela será negativa,o que não se pede
c) (x + 6)^7 . (6x - 2)^4 . (4x + 5)^10 ≤ 0
Expandir esta imagem Ver em tamanho real
Imagem da minha resolução da questão.Resposta do livro: S = {x∈ℝ | x ≤ -6 ou x = 1/3 ou x = -5/4}
Nessa resposta, por que os pontos -5/4 e 1/3 foram incluídos?
FernandoFRN- Iniciante
- Mensagens : 11
Data de inscrição : 03/07/2019
Idade : 22
Localização : Belém-PA
Re: Inequações-produto
por lejandrocohen Sex 27 Mar 2020, 10:30
Perdoe meu erro, você está correto,pois X=-4/5 também é raíz da primeira equação sendo assim o conjunto solução S=S = {x∈ℝ | x ≥ 2/7 ou x= -4/5},visto que a primeira equação (5x + 4)⁴ . (7x - 2)³ ≥ 0,torna zero,tornado assim [0.(7x - 2)³ ≥ 0],sendo verdadeiro
Assim como na questão (x + 6)^7 . (6x - 2)^4 . (4x + 5)^10 ≤ 0
S = {x∈ℝ | x ≤ -6 ou x = 1/3 ou x = -5/4}
Tornando um dos membros da equação igual a zero
Creio que a resposta do livro no primeiro ex, esteja errada!
Perdoe meu equívoco
Assim como na questão (x + 6)^7 . (6x - 2)^4 . (4x + 5)^10 ≤ 0
S = {x∈ℝ | x ≤ -6 ou x = 1/3 ou x = -5/4}
Tornando um dos membros da equação igual a zero
Creio que a resposta do livro no primeiro ex, esteja errada!
Perdoe meu equívoco
lejandrocohen- Padawan
- Mensagens : 54
Data de inscrição : 08/07/2019
Idade : 25
Localização : Natal-RN
Re: Inequações-produto
por FernandoFRN Sex 27 Mar 2020, 11:04
Obrigado mesmo assim.lejandrocohen escreveu:Perdoe meu erro, você está correto,pois X=-4/5 também é raíz da primeira equação sendo assim o conjunto solução S=S = {x∈ℝ | x ≥ 2/7 ou x= -4/5},visto que a primeira equação (5x + 4)⁴ . (7x - 2)³ ≥ 0,torna zero,tornado assim [0.(7x - 2)³ ≥ 0],sendo verdadeiro
Assim como na questão (x + 6)^7 . (6x - 2)^4 . (4x + 5)^10 ≤ 0
S = {x∈ℝ | x ≤ -6 ou x = 1/3 ou x = -5/4}
Tornando um dos membros da equação igual a zero
Creio que a resposta do livro no primeiro ex, esteja errada!
Perdoe meu equívoco
Creio que o erro do item a) tenha sido colocar "maior ou igual" em vez de "maior", tanto na pergunta quanto na resposta. Desconsiderando "ou igual", o item a) está correto.
FernandoFRN- Iniciante
- Mensagens : 11
Data de inscrição : 03/07/2019
Idade : 22
Localização : Belém-PA
Re: Inequações-produto
por Elcioschin Sex 27 Mar 2020, 11:55
Fernando
Todo número real elevado a um expoente par é positivo ou nulo.
(5.x + 4)⁴ . (7.x - 2)³ ≥ 0
O 1º fator está com expoente 4 (par) logo ele é sempre positivo ou nulo, atendendo à inequação. Logo, ele NÃO influencia no resultado da inequação.
Logo, o sinal da inequação só depende do 2º fator: (7.x - 2)³
Assim, não é necessário fazer a tabela de sinais (varal) para o 1º fator, só para o 2º fator
Este fator será nulo para x = 2/7, positivo para x > 2/7 e negativo para x < 2/7
A solução da inequação, portanto, é x ≥ 2/7
O mesmo vale para a segunda inequação: x ≤ -6
Todo número real elevado a um expoente par é positivo ou nulo.
(5.x + 4)⁴ . (7.x - 2)³ ≥ 0
O 1º fator está com expoente 4 (par) logo ele é sempre positivo ou nulo, atendendo à inequação. Logo, ele NÃO influencia no resultado da inequação.
Logo, o sinal da inequação só depende do 2º fator: (7.x - 2)³
Assim, não é necessário fazer a tabela de sinais (varal) para o 1º fator, só para o 2º fator
Este fator será nulo para x = 2/7, positivo para x > 2/7 e negativo para x < 2/7
A solução da inequação, portanto, é x ≥ 2/7
O mesmo vale para a segunda inequação: x ≤ -6
Elcioschin- Grande Mestre
- Mensagens : 73163
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
RodriguesRapati2023 gosta desta mensagem
Re: Inequações-produto
por FernandoFRN Sex 27 Mar 2020, 12:22
O mesmo também vale para o item d) da mesma questão?Elcioschin escreveu:Fernando
Todo número real elevado a um expoente par é positivo ou nulo.
(5.x + 4)⁴ . (7.x - 2)³ ≥ 0
O 1º fator está com expoente 4 (par) logo ele é sempre positivo ou nulo, atendendo à inequação. Logo, ele NÃO influencia no resultado da inequação.
Logo, o sinal da inequação só depende do 2º fator: (7.x - 2)³
Assim, não é necessário fazer a tabela de sinais (varal) para o 1º fator, só para o 2º fator
Este fator será nulo para x = 2/7, positivo para x > 2/7 e negativo para x < 2/7
A solução da inequação, portanto, é x ≥ 2/7
O mesmo vale para a segunda inequação: x ≤ -6
d) (5x - 1) . (2x + 6)^8 . (4 - 6x)^6 ≥ 0
Imagem da minha resolução da questão.Resposta do livro: S = {x∈ℝ | x ≥ 1/5 ou x = -3}
Nesse caso seriam dois itens errados na mesma questão.
FernandoFRN- Iniciante
- Mensagens : 11
Data de inscrição : 03/07/2019
Idade : 22
Localização : Belém-PA
Re: Inequações-produto
por Elcioschin Sex 27 Mar 2020, 12:41
Na 1ª inequação a solução completa é x ≥ 2/7 e x = - 4/5
Ou o gabarito está incompleto ou o sinal da inequação deveria ser >
Na 2ª inequação a solução completa é: x ≤ -6, x = 1/3 e x = - 5/4
Na 3ª inequação:
(5.x - 1) . (2.x + 6)^8 . (4 - 6.x)^6 ≥ 0
A solução completa é: x ≥ 1/5, x = - 3 e x = 2/3: O gabarito está incompleto
Ou o gabarito está incompleto ou o sinal da inequação deveria ser >
Na 2ª inequação a solução completa é: x ≤ -6, x = 1/3 e x = - 5/4
Na 3ª inequação:
(5.x - 1) . (2.x + 6)^8 . (4 - 6.x)^6 ≥ 0
A solução completa é: x ≥ 1/5, x = - 3 e x = 2/3: O gabarito está incompleto
Elcioschin- Grande Mestre
- Mensagens : 73163
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tópicos semelhantes» Inequações de 2º grau e Inequações Produto
» Inequações-produto
» Inequações produto
» Inequações produto
» Inequações Produto e Quociente
» Inequações-produto
» Inequações produto
» Inequações produto
» Inequações Produto e Quociente
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
