GA - Coordenadas dos pontos

por j_lucasps Sáb 14 Mar 2020, 10:11

Certa empresa irá construir uma sede própria para a sua filial em uma grande cidade brasileira. Com o intuito de inovar no projeto do edifício que abrigará a filial e impressionar os novos clientes, os engenheiros responsáveis decidiram que o prédio teria base quadrada e seria construído de forma que a diagonal da base fosse paralela à calçada, como na figura 1, a seguir.

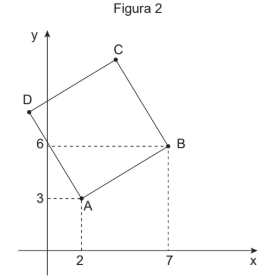
Para iniciar o projeto, os engenheiros usaram um plano cartesiano, figura 2, para facilitar os cálculos e determinar exatamente as coordenadas da base do edifício.

Contudo, antes de viajar de volta para a matriz da empresa, o engenheiro calculista só especificou que o ponto A = (2, 3) e que o ponto B = (7, 6).

Para prosseguirem com o projeto, os demais engenheiros determinaram que as coordenadas dos pontos C e D são, respectivamente,

(A) (4, 11) e (-1, Cool

(B) (4, 11) e (-1, 9)

(C) (3, 12) e (-2, 7)

(D) (3, 11) e (-2, Cool

(E) (4, 13) e (-1, 7)

por **Medeiros** Sáb 14 Mar 2020, 13:50

Para mim o mais fácil é supor que os pontos vértice estão num plano de Argand-Gauss e suas coordenadas são números complexos.

A diferença entre dois pontos resulta num vetor livre orientado conforme os pontos, ou seja, num outro número complexo cujo módulo é a distância entre estes pontos. E cada vez que multiplicamos esse número complexo por i, rotacionamos o vetor 90° no sentido anti-horário.

Basta, então, somar este vetor (número complexo) ao ponto de onde se quer partir para chegar ao outro vértice.

por **Elcioschin** Sáb 14 Mar 2020, 14:48

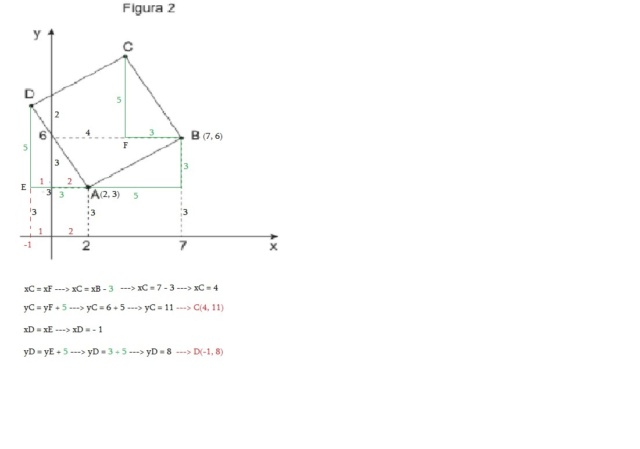
Um outro modo simples, considerando que cada reta de um lado do quadrado é perpendicular à reta do lado adjacente

De A para B andamos 5 para a direita e 3 para cima:

De B para C devemos andar 3 para a esquerda e 5 para cima:

xC = 7 - 3 = 4
yC = 6 + 5 = 11 ---> C(4, 11)

De A para D devemos andar 3 para a esquerda e 5 para cima:

xD = 2 - 3 = -1
yD = 3 + 5 = 8 ---> D(-1, 8 )

por j_lucasps Dom 15 Mar 2020, 07:37

Elcioschin, por que "considerando que cada reta de um lado do quadrado é perpendicular à reta do lado adjacente"?

por **Elcioschin** Dom 15 Mar 2020, 10:27

1) O quadrado tem 4 ângulos retos; isto significa que cada lado é perpendicular aos dois lados ajacentes

2) Vamos calcular o coeficiente angular da reta que contém o lado AB:

m = (yB - yA)/(xB - xA) ---> m = (6 - 3)/(7 - 2) ---> m = 3/5

Pela regra do perpendicularismo de duas retas, o coeficiente angular da reta BC vale m' = - 5/3

Isto significa que: De B para C devemos andar 3 para a esquerda e 5 para cima:

xC = 7 - 3 = 4
yC = 6 + 5 = 11 ---> C(4, 11)

De modo similar calcula-se D(-1, 8 )

por j_lucasps Dom 15 Mar 2020, 13:27

Ao calcular m' a partir de m, usando a regra da perpendicularidade de duas retas, m' deve ser calculado, obrigatoriamente, por: m' = yB - yC / xB - xC ?

Fiz inicialmente m' = yC - yB / xC - xB e obtive um valor incorreto p xC e yC.

por **Elcioschin** Dom 15 Mar 2020, 15:05

Não precisa fazer isto:

Já sabemos que para a reta AB ---> m = 3/5

Fórmula da perpendicularidade:

m.m' = -1 ---> m' = - 1/m ---> m' = -1/(3/5) ---> m' = - 5/3

por Gemma Galgani Qui 09 Set 2021, 13:42

Elcioschin escreveu:Um outro modo simples, considerando que cada reta de um lado do quadrado é perpendicular à reta do lado adjacente

De A para B andamos 5 para a direita e 3 para cima:

De B para C devemos andar 3 para a esquerda e 5 para cima:

xC = 7 - 3 = 4
yC = 6 + 5 = 11 ---> C(4, 11)

De A para D devemos andar 3 para a esquerda e 5 para cima:

xD = 2 - 3 = -1
yD = 3 + 5 = 8 ---> D(-1, 8 )

olá !!1 pq calculamos a equação da reta?? não daria para fazer só com o lado do quadrado não?? descobri q ele é 6.... mas n desenrolei

por Gemma Galgani Qui 09 Set 2021, 13:43

Elcioschin escreveu:1) O quadrado tem 4 ângulos retos; isto significa que cada lado é perpendicular aos dois lados ajacentes

2) Vamos calcular o coeficiente angular da reta que contém o lado AB:

m = (yB - yA)/(xB - xA) ---> m = (6 - 3)/(7 - 2) ---> m = 3/5

Pela regra do perpendicularismo de duas retas, o coeficiente angular da reta BC vale m' = - 5/3

Isto significa que: De B para C devemos andar 3 para a esquerda e 5 para cima:

xC = 7 - 3 = 4
yC = 6 + 5 = 11 ---> C(4, 11)

De modo similar calcula-se D(-1, 8 )

olá, pq usasse a equaçao da reta???? achei o lado do quadrado- que deu 6- mas n sai dai