Triângulo

Duas das alturas de um triângulo acutângulo intersectam os lados, em relação aos quais são traçados,segundo segmentos que medem 5,3,2 e x, nessa ordem. o valor de x é igual:

Respota= 10

Desenhe um triângulo acutângulo ABC, trace duas alturas (segmentos de reta que ligam o vértice ao lado oposto, sendo perpendicular a este ou ao seu prolongamento), chame de D e E os vértices formados pelos lados e alturas, além de chamar os lados AB, BD e AE de, respectivamente, w, z e y. O seu triângulo ficará assim:



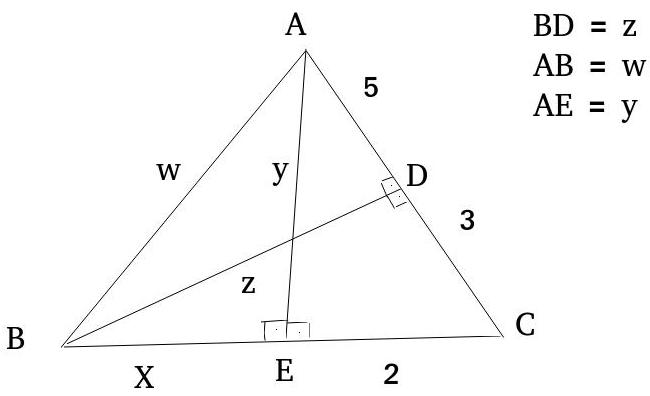
Primeiramente, calcule o valor de y:

    Pelo Teorema de Pitágoras: y² + 2²  = (5 + 3)²
                                                 y = √60


Depois, calcule o valor de z e w :
    

   Valor de z:
        
      
          Pelo Teorema de Pitágoras temos que: z² + 3² = (x + 2)²
                                                                       z = √(x² + 4x - 5)

    Valor de w:



         Também utilizando o Teorema de Pitágoras: w² = z² + 5²

                                                                                w = √(x² + 4x + 20)

Por fim, descobriremos o valor de x pelo Teorema de Pitágoras:
 
          w² = y² + x²
          x² = w² - y²
          x² = x² + 4x + 20 - 60
          x = 10