Canadá
5 participantes
Página 2 de 2
Página 2 de 2 • 
1, 2
Canadá
por Vitor Ahcor Sáb 14 Set 2019, 15:45
Relembrando a primeira mensagem :
Se a,b e c são as raízes da equação x³ - x² - x -1 = 0
I. Mostre que a, b e c são distintas;
II. Mostre que\frac{a^{1982}-b^{1982}}{a-b} + \frac{b^{1982}-c^{1982}}{b-c} + \frac{c^{1982}-a^{1982}}{c-a} é um número inteiro.
*Obs: No item I, imagino que basta verificar que as raízes de 3x² -2x -1 = 0 não são raízes da equação, porém, não estou conseguindo provar o item II.
Se a,b e c são as raízes da equação x³ - x² - x -1 = 0
I. Mostre que a, b e c são distintas;
II. Mostre que
*Obs: No item I, imagino que basta verificar que as raízes de 3x² -2x -1 = 0 não são raízes da equação, porém, não estou conseguindo provar o item II.
Última edição por vitorrochap2013 em Dom 15 Set 2019, 22:23, editado 1 vez(es)
____________________________________________
Cha-la head-cha-la
Vitor Ahcor- Monitor
- Mensagens : 780
Data de inscrição : 21/12/2018
Idade : 24
Localização : Taurdal
Re: Canadá
por fantecele Dom 15 Set 2019, 10:12
Na I o que eu tentaria fazer era supor que, primeiro, as 3 raízes eram iguais, depois eu faria que 2 delas eram iguais, calculava elas e depois tentaria chegar a algum "absurdo", mostrando assim que não podemos ter raízes iguais.
Na II eu estava fazendo aqui, e não estava saindo saindo nada, então comecei a calcular para expoentes diferente de 1982, como para 1, para 2, para 3, para 4 e percebi que todos eles estavam dando números inteiros, daí tentei fazer para um caso geral, por que se eu mostrasse que era verdadeiro para o caso geral, então teria que ser válido para 1982 (ou eu não chegaria em nada né, mas tentei ver se conseguia mostrar isso ali), então eu considerei:
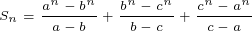
Daí, calculando para alguns valores pequenos, S1 = 3, S2 = 2, S3 = 5, S4 = 10.
Agora, perceba que, de x³ - x² - x - 1 = 0, temos que:
+\left&space;(&space;a^{n-2}-b^{n-2}&space;\right&space;)+\left&space;(&space;a^{n-3}-b^{n-3}&space;\right&space;)\\b^n-c^n=\left&space;(&space;b^{n-1}-c^{n-1}&space;\right&space;)+\left&space;(&space;b^{n-2}-c^{n-2}&space;\right&space;)+\left&space;(&space;b^{n-3}-c^{n-3}&space;\right&space;)\\c^n-a^n=\left&space;(&space;c^{n-1}-a^{n-1}&space;\right&space;)+\left&space;(&space;c^{n-2}-a^{n-2}&space;\right&space;)+\left&space;(&space;c^{n-3}-a^{n-3}&space;\right&space;) "\tiny \\a^3-a^2-a-1=0\,\,\,\,*a^{n-3}\rightarrow a^n=a^{n-1}+a^{n-2}+a^{n-3}\\b^3-b^2-b-1=0\,\,\,\,\,\,*b^{n-3}\rightarrow b^n=b^{n-1}+b^{n-2}+b^{n-3}\\\\a^n-b^n=\left ( a^{n-1}-b^{n-1} \right )+\left ( a^{n-2}-b^{n-2} \right )+\left ( a^{n-3}-b^{n-3} \right )\\b^n-c^n=\left ( b^{n-1}-c^{n-1} \right )+\left ( b^{n-2}-c^{n-2} \right )+\left ( b^{n-3}-c^{n-3} \right )\\c^n-a^n=\left ( c^{n-1}-a^{n-1} \right )+\left ( c^{n-2}-a^{n-2} \right )+\left ( c^{n-3}-a^{n-3} \right )")
Na equação para Sn, nós iremos encontrar que:
+\\\left&space;(&space;\frac{a^{n-2}-b^{n-2}}{a-b}+\frac{b^{n-2}-c^{n-2}}{b-c}+\frac{c^{n-2}-a^{n-2}}{c-a}&space;\right&space;)+\\\left&space;(&space;\frac{a^{n-3}-b^{n-3}}{a-b}+\frac{b^{n-3}-c^{n-3}}{b-c}+\frac{c^{n-3}-a^{n-3}}{c-a}&space;\right&space;)\\\\S_n=S_{n-1}+S_{n-2}+S_{n-3} "\tiny \\S_n=\frac{a^n-b^n}{a-b}+\frac{b^n-c^n}{b-c}+\frac{c^n-b^n}{c-b}\\\\S_n=\left ( \frac{a^{n-1}-b^{n-1}}{a-b}+\frac{b^{n-1}-c^{n-1}}{b-c}+\frac{c^{n-1}-a^{n-1}}{c-a} \right )+\\\left ( \frac{a^{n-2}-b^{n-2}}{a-b}+\frac{b^{n-2}-c^{n-2}}{b-c}+\frac{c^{n-2}-a^{n-2}}{c-a} \right )+\\\left ( \frac{a^{n-3}-b^{n-3}}{a-b}+\frac{b^{n-3}-c^{n-3}}{b-c}+\frac{c^{n-3}-a^{n-3}}{c-a} \right )\\\\S_n=S_{n-1}+S_{n-2}+S_{n-3}")
Daí conseguimos uma relação de recorrência para Sn, então podemos mostrar, por principio de indução forte, que Sn será inteiro, basta então considerar que para k ≤ n-1 é verdade, (que no caso seria considerar que Sk é inteiro para aqueles valores de k, como você pode ter percebido quando calculei para os valores 1, 2, 3 e 4), daí basta mostrar que será verdadeiro para Sn, mas perceba que, como eu havia dito, para k ≤ n-1 a relação Sk é inteira, então, na expressão encontrada acima para Sn, iremos ter a soma de 3 inteiros, que também é um inteiro, então temos que Sn também é inteiro.
Dessa forma, se Sn é inteiro para todo n então S1982 também será inteiro.
Acho que é isso, qualquer coisa é só perguntar.
Na II eu estava fazendo aqui, e não estava saindo saindo nada, então comecei a calcular para expoentes diferente de 1982, como para 1, para 2, para 3, para 4 e percebi que todos eles estavam dando números inteiros, daí tentei fazer para um caso geral, por que se eu mostrasse que era verdadeiro para o caso geral, então teria que ser válido para 1982 (ou eu não chegaria em nada né, mas tentei ver se conseguia mostrar isso ali), então eu considerei:
Daí, calculando para alguns valores pequenos, S1 = 3, S2 = 2, S3 = 5, S4 = 10.
Agora, perceba que, de x³ - x² - x - 1 = 0, temos que:
Na equação para Sn, nós iremos encontrar que:
Daí conseguimos uma relação de recorrência para Sn, então podemos mostrar, por principio de indução forte, que Sn será inteiro, basta então considerar que para k ≤ n-1 é verdade, (que no caso seria considerar que Sk é inteiro para aqueles valores de k, como você pode ter percebido quando calculei para os valores 1, 2, 3 e 4), daí basta mostrar que será verdadeiro para Sn, mas perceba que, como eu havia dito, para k ≤ n-1 a relação Sk é inteira, então, na expressão encontrada acima para Sn, iremos ter a soma de 3 inteiros, que também é um inteiro, então temos que Sn também é inteiro.
Dessa forma, se Sn é inteiro para todo n então S1982 também será inteiro.
Acho que é isso, qualquer coisa é só perguntar.
fantecele- Fera
- Mensagens : 1225
Data de inscrição : 14/09/2014
Idade : 27
Localização : Nova Venécia-ES, Brasil
Re: Canadá
por Vitor Ahcor Dom 15 Set 2019, 14:09
Sacada muito boa fantecele!
Valeu demais!!
Valeu demais!!
____________________________________________
Cha-la head-cha-la
Vitor Ahcor- Monitor
- Mensagens : 780
Data de inscrição : 21/12/2018
Idade : 24
Localização : Taurdal
Re: Canadá
por Nickds12 Seg 16 Set 2019, 13:49
Eu até disse que não comento mais, mas apenas uma observação:
Já existem teoremas para esse tipo de divisão com números inteiros e ímpares. Como eu disse, além de eu não gostar dessa demagogia matemática, resolver essa questão envolve trabalhar com número reais e complexos. Veja a prova do teorema de x^n+y^n/(x+y) (elevado a números ímpares) e como não é possível provar desse jeito de forma "normal".
x^2n+1 + y^2n+1 = (x+y)*(x2n...+y2n) = (x+y)P(2n+1)(x,y) (polinomio de grau 2n+1)
x^1 + y^1 = x + y (a menor configuração da sequência, que no caso do problema será o divisor)
Mas
x^2n+3 + y^2n+3 = (x+y)P(2n+2)(x,y)
E
(x^2n+1 + y^2n+1)*(x^2 + y^2) = x^(2n+3) + x^2*y^(2n+1) + x^2*y^2n+1 + y^2n+3
Mas
x^2n+3 + y^2n+3 = (x+y)(x^2 + y^2)P(2n)(x,y) - x^2*y^2 (y^2n-1 + x^2n-1)
E como
y^2n-1 + x^2n-1 = (x+y)P(2n-2)
(x+y)P(2n+2)(x,y) = (x+y)(x^2 + y^2)P(2n)(x,y) - x^2*y^2P(2n-2))(x,y)
E por indução forte, prova-se o teorema.
Veja que se fosse uma subtração entre números inteiros
Eu teria
- x^(n+1) - x^2*y^(n+1), não sendo possível colocar a representação do polinômio (x+y)P(2n-2).
Ou seja, (x^n-y^n)/(x-y) precisa ter números complexos em suas variáveis.
Já existem teoremas para esse tipo de divisão com números inteiros e ímpares. Como eu disse, além de eu não gostar dessa demagogia matemática, resolver essa questão envolve trabalhar com número reais e complexos. Veja a prova do teorema de x^n+y^n/(x+y) (elevado a números ímpares) e como não é possível provar desse jeito de forma "normal".
x^2n+1 + y^2n+1 = (x+y)*(x2n...+y2n) = (x+y)P(2n+1)(x,y) (polinomio de grau 2n+1)
x^1 + y^1 = x + y (a menor configuração da sequência, que no caso do problema será o divisor)
Mas
x^2n+3 + y^2n+3 = (x+y)P(2n+2)(x,y)
E
(x^2n+1 + y^2n+1)*(x^2 + y^2) = x^(2n+3) + x^2*y^(2n+1) + x^2*y^2n+1 + y^2n+3
Mas
x^2n+3 + y^2n+3 = (x+y)(x^2 + y^2)P(2n)(x,y) - x^2*y^2 (y^2n-1 + x^2n-1)
E como
y^2n-1 + x^2n-1 = (x+y)P(2n-2)
(x+y)P(2n+2)(x,y) = (x+y)(x^2 + y^2)P(2n)(x,y) - x^2*y^2P(2n-2))(x,y)
E por indução forte, prova-se o teorema.
Veja que se fosse uma subtração entre números inteiros
Eu teria
- x^(n+1) - x^2*y^(n+1), não sendo possível colocar a representação do polinômio (x+y)P(2n-2).
Ou seja, (x^n-y^n)/(x-y) precisa ter números complexos em suas variáveis.
Nickds12- Mestre Jedi
- Mensagens : 577
Data de inscrição : 31/08/2019
Idade : 27
Localização : RJ
Página 2 de 2 • 1, 2
Tópicos semelhantesPágina 2 de 2
Permissões neste sub-fórum
Não podes responder a tópicos
