EFOMM 2020 - Geometria Espacial

por GBRezende Ter 20 Ago 2019, 12:01

Seja a esfera de raio R inscrita na pirâmide quadrangular regular de aresta base 2cm e aresta lateral √(38) cm. Sabendo-se que a esfera tangencia todas as faces da pirâmide, o valor de R, em cm, é

\frac{\sqrt{37}-1}{6}
Este gabarito é provisório. Estou ansioso por essa resolução!

por **Medeiros** Ter 20 Ago 2019, 12:50

A altura do triângulo da face lateral é V37.

A altura da pirâmide é V36 = 6.

Semelhança de triângulos.:
R/1 = (6 - R)/V37

Basta racionalizar; o gabarito confere.

por **Elcioschin** Ter 20 Ago 2019, 13:06

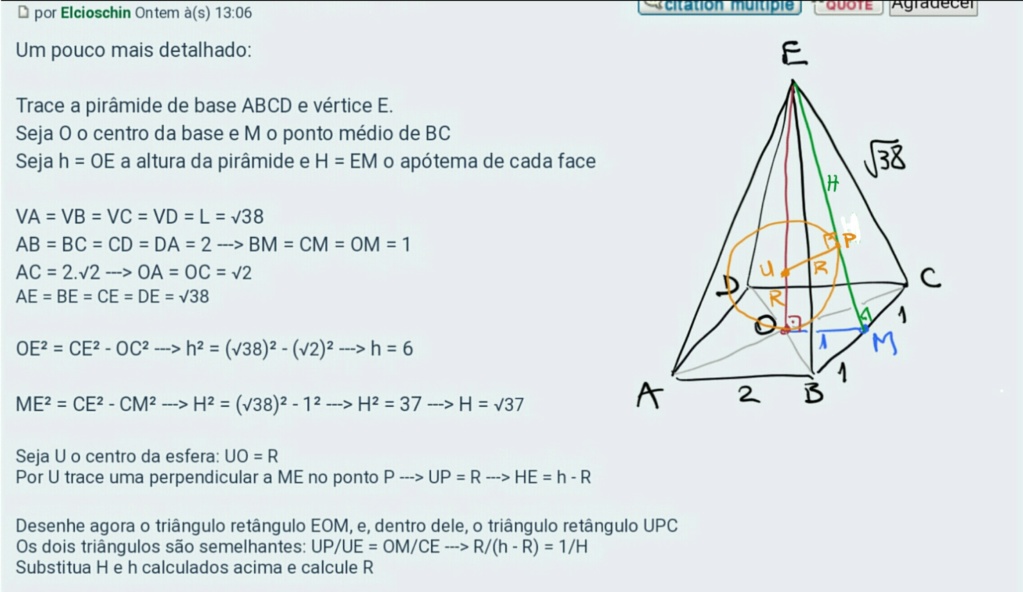
Um pouco mais detalhado:

Trace a pirâmide de base ABCD e vértice E.
Seja O o centro da base e M o ponto médio de BC
Seja h = OE a altura da pirâmide e H = EM o apótema de cada face

VA = VB = VC = VD = L = √38
AB = BC = CD = DA = 2 ---> BM = CM = OM = 1
AC = 2.√2 ---> OA = OC = √2
AE = BE = CE = DE = √38

OE² = CE² - OC² ---> h² = (√38)² - (√2)² ---> h = 6

ME² = CE² - CM² ---> H² = (√38)² - 1² ---> H² = 37 ---> H = √37

Seja U o centro da esfera: UO = R
Por U trace uma perpendicular a ME no ponto P ---> UP = R ---> HE = h - R

Desenhe agora o triângulo retângulo EOM, e, dentro dele, o triângulo retângulo UPC
Os dois triângulos são semelhantes: UP/UE = OM/CE ---> R/(h - R) = 1/H
Substitua H e h calculados acima e calcule R