EFOMM 2020 Área do triângulo
5 participantes
Página 1 de 1
EFOMM 2020 Área do triângulo
por Isabel Leal Ter 20 Ago 2019, 13:52
Sejam a circunferência C1, com centro em A e raio 1, e a circunferência C2 que passa por A, com centro em B e raio 2. Sabendo-se que D é o ponto médio do segmento AB, E é um dos pontos de interseção entre C1 e C2, e F é a interseção da reta ED com a circunferência C2, o valor da área do triângulo AEF, em unidades de área, é :
Resp: (3raiz15)/8
Resp: (3raiz15)/8
Isabel Leal- Padawan
- Mensagens : 69
Data de inscrição : 14/03/2016
Idade : 26
Localização : Cabo Frio
Re: EFOMM 2020 Área do triângulo
por Rory Gilmore Ter 20 Ago 2019, 16:28
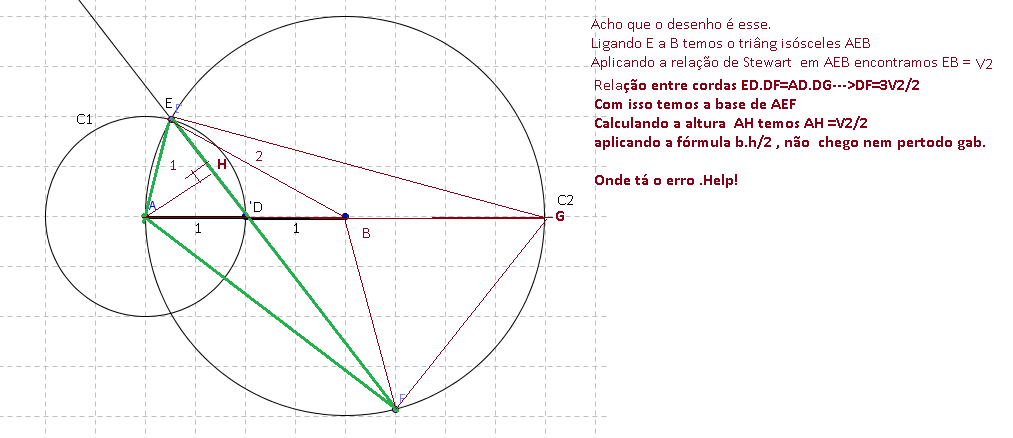
I) D é ponto da circunferência menor.
II) Prolongue AB até o ponto P na circunferência maior.
III) No triângulo retângulo APE desenhe EB que é mediana relativa a hipotenusa.
IV) Encontre o cateto EP do triângulo APE.
V) Os ângulos dos vértices F e P são congruentes = (arco EA)/2
VI) Encontre o seno do ângulos citados pelo triângulo retângulo referido.
VII) Aplique semelhança de triângulos e se necessário trigonometria para encontrar os lados AF e EF.
VIII) Calcule a área de AEF pela fórmula:
S = (AF.EF.sen ^F)/2
II) Prolongue AB até o ponto P na circunferência maior.
III) No triângulo retângulo APE desenhe EB que é mediana relativa a hipotenusa.
IV) Encontre o cateto EP do triângulo APE.
V) Os ângulos dos vértices F e P são congruentes = (arco EA)/2
VI) Encontre o seno do ângulos citados pelo triângulo retângulo referido.
VII) Aplique semelhança de triângulos e se necessário trigonometria para encontrar os lados AF e EF.
VIII) Calcule a área de AEF pela fórmula:
S = (AF.EF.sen ^F)/2
Rory Gilmore- Monitor
- Mensagens : 1878
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
raimundo pereira- Grupo
Velhos amigos do Fórum
- Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: EFOMM 2020 Área do triângulo
por raimundo pereira Ter 20 Ago 2019, 21:11
Ôpa! encontrei o erro. Na 1a resol.errei no cáculo da relação de Stewart.
Invertir o desenho, e recalculando encontrei o erro.
Sinto que existe uma resol mais simples , mas não consegui enxergar.
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: EFOMM 2020 Área do triângulo
por Medeiros Qua 21 Ago 2019, 10:26
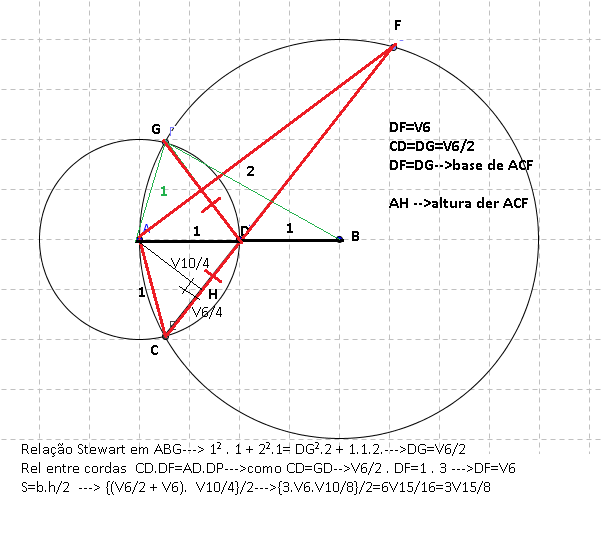
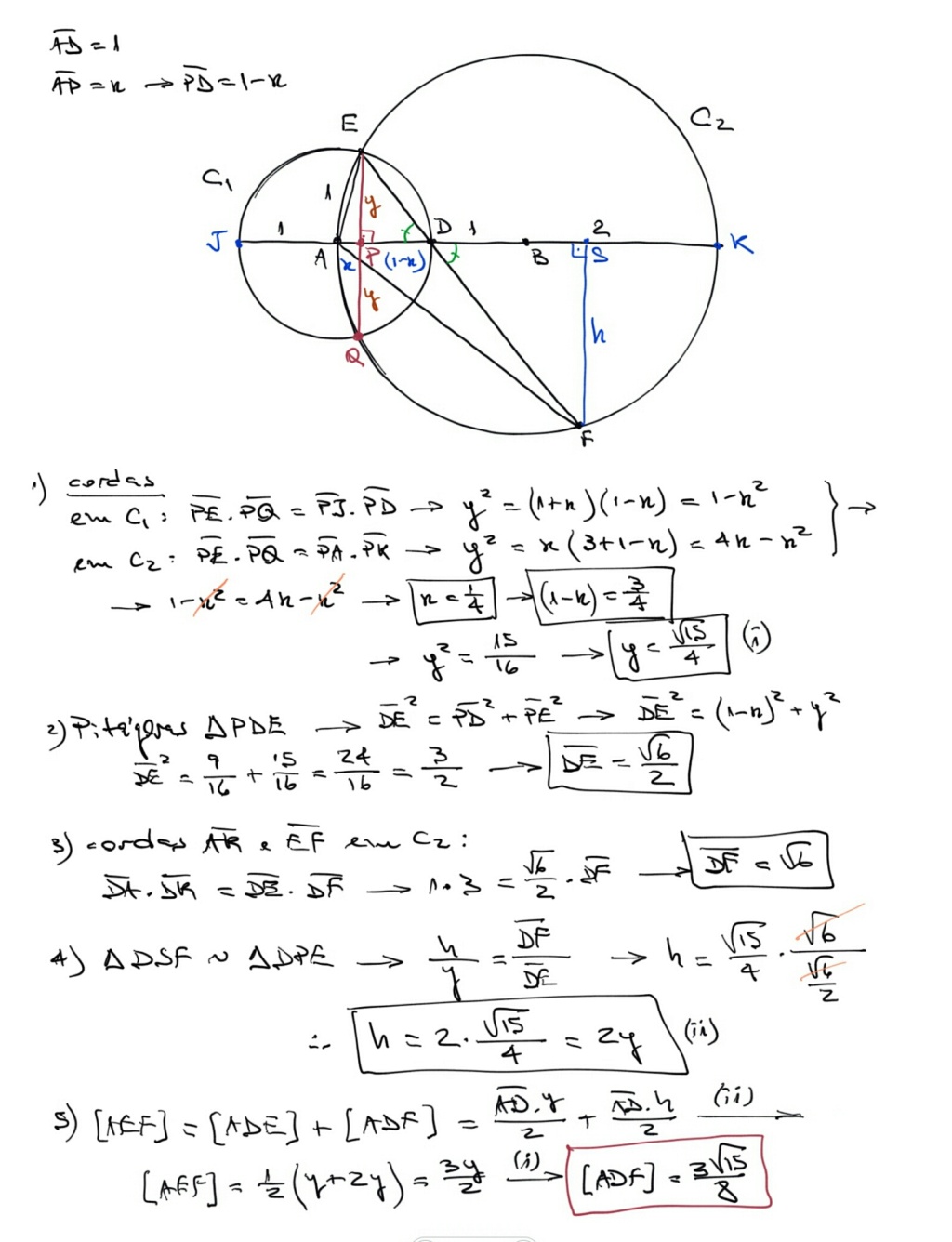
Dá pra fazer sem Stewart, apenas com teoria das cordas, Pitágoras e semelhança de triângulos. Hoje à noite devo chegar mais cedo e faço.
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: EFOMM 2020 Área do triângulo
por Medeiros Qui 22 Ago 2019, 01:06
Se a imagem estiver pequena, clique em "Expandir esta imagem" que ela se conformará à coluna do site.
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: EFOMM 2020 Área do triângulo
por Medeiros Sex 23 Ago 2019, 02:31
é uma boa sacada, Raimundo. Só que vc precisa mostrar como obter a medida AR.
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: EFOMM 2020 Área do triângulo
por raimundo pereira Sex 23 Ago 2019, 12:56
Oi Medeiros,
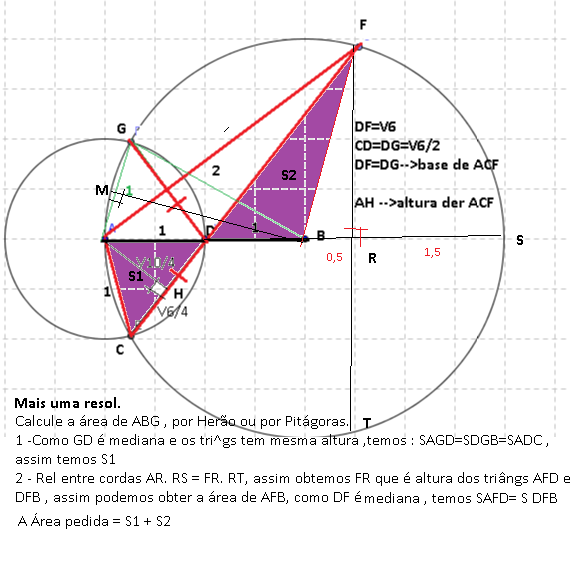
Por equialencia de áreas, o triâng BFS tem exatamente o dobro da área de DFB.
Ou seja: temos 3 triângs congruentes.
Assim FR é a altura do triâng DFS . Como a base de DFS=3 e DFS é isósceles ,
DR=1,5 e AR=1 + 1,5=2,5
Por equialencia de áreas, o triâng BFS tem exatamente o dobro da área de DFB.
Ou seja: temos 3 triângs congruentes.
Assim FR é a altura do triâng DFS . Como a base de DFS=3 e DFS é isósceles ,
DR=1,5 e AR=1 + 1,5=2,5
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: EFOMM 2020 Área do triângulo
por SnoopLy Sex 23 Ago 2019, 15:32
Uma outra solução
Pra melhor visualização, veja a imagem em tamanho real
Pra melhor visualização, veja a imagem em tamanho real
SnoopLy- Jedi
- Mensagens : 225
Data de inscrição : 23/02/2017
Idade : 24
Localização : Brasil, Rio de Janeiro
Tópicos semelhantes» [EFOMM 2010]-Área do triangulo
» EFOMM 2015 - Área de triângulo
» [EFOMM 2020] Ondulatória
» (EFOMM 2020) Cubo e esferas
» EFOMM 2020 - Geometria Espacial
» EFOMM 2015 - Área de triângulo
» [EFOMM 2020] Ondulatória
» (EFOMM 2020) Cubo e esferas
» EFOMM 2020 - Geometria Espacial
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
