UFRGS - analítica
2 participantes
Página 1 de 1
UFRGS - analítica
por folettinhomed Ter 13 Ago 2019, 23:50
Considere, na figura abaixo, a região sombreada limitada por uma reta e pelo gráfico de uma função quadrática.
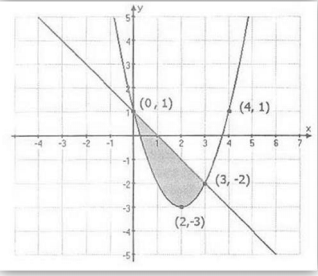
As coordenadas dos pontos (x,y) dessa região verificam as desigualdades:
(A) x²– 4x + 1 ≤ y ≤ 1 – x
(B) x² – x + 4 ≥ y ≥ 1 – x
(C) x² – 2x + 1 ≤ y ≤ 1 – x
(D) x² – 4x – 1 ≥ y≥ 1 – x
(E) x² – 2x + 1≥ y ≥ 1 + x
Gente, eliminei a B, D e E pela parábola estar abaixo da região sombreada e pela reta estar acima da região sombreada, ou seja, pela parábola ser menor ou igual que y e pela reta ser maior ou igual a y, mas não entendi nada de como obter os valores. Poderiam me explicar?
As coordenadas dos pontos (x,y) dessa região verificam as desigualdades:
(A) x²– 4x + 1 ≤ y ≤ 1 – x
(B) x² – x + 4 ≥ y ≥ 1 – x
(C) x² – 2x + 1 ≤ y ≤ 1 – x
(D) x² – 4x – 1 ≥ y≥ 1 – x
(E) x² – 2x + 1≥ y ≥ 1 + x
Gente, eliminei a B, D e E pela parábola estar abaixo da região sombreada e pela reta estar acima da região sombreada, ou seja, pela parábola ser menor ou igual que y e pela reta ser maior ou igual a y, mas não entendi nada de como obter os valores. Poderiam me explicar?
Última edição por folettinhomed em Qua 14 Ago 2019, 12:37, editado 1 vez(es)
folettinhomed- Mestre Jedi
- Mensagens : 988
Data de inscrição : 23/02/2019
Idade : 24
Localização : Santa Cruz do Sul, RS, Brasil
Re: UFRGS - analítica
por Medeiros Qua 14 Ago 2019, 03:07
o exercício te obriga a achar a equação da reta (r) e a da parábola (p), não tem outro jeito.
r:
y = -(x - 1) -----> y = -x + 1
p:
y = a.(x - xV)2 + yV .............. forma canônica da eq da parábola
V(2, -3) -----> y = a.(x - 2)2 - 3
(0, 1) ∈ p -----> 1 = a.(0 - 2)2 - 3 -----> a = 1
.:. y = 1.(x - 2)2 - 3 -----> y = x2 - 4x + 1
na região delimitada devemos ter o y maior ou igual a parábola e menor ou igual à reta. Portanto
x2 - 4x + 1 ≤ y ≤ -x + 1
r:
y = -(x - 1) -----> y = -x + 1
p:
y = a.(x - xV)2 + yV .............. forma canônica da eq da parábola
V(2, -3) -----> y = a.(x - 2)2 - 3
(0, 1) ∈ p -----> 1 = a.(0 - 2)2 - 3 -----> a = 1
.:. y = 1.(x - 2)2 - 3 -----> y = x2 - 4x + 1
na região delimitada devemos ter o y maior ou igual a parábola e menor ou igual à reta. Portanto
x2 - 4x + 1 ≤ y ≤ -x + 1
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
joice21 gosta desta mensagem
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
