Retas perpendiculares

por **Emanuel Dias** Sex 02 Ago 2019, 00:28

Determine k de modo que as retas de equações e (2k - 2)x + (k - 1)y + k = O e X + (k - 3)y - 2k = 0 sejam perpendiculares.

Gabarito: k=1.

Primeiro que se k for igual a 1 a primeira equação vira 1=0, absurdo.

Eu cheguei a k=1 ou k=5 mas usando Geogebra quando k=5 as duas equações não são perpendiculares.

por Alysonaa Sex 02 Ago 2019, 00:55

Resolvi a questão por geometria analítica, porém, o resultado foi 1/2, diferente do teu gabarito, claro.

Primeiramente, organizei as equações:

y(k-1)=x(-2k+2)-k

y(k-3)=-x+2k

Após isso, usei as relações das retas quanto suas posições, o que consiste em:

Perpendiculares: m1.m2= -1

Dado que:

y=m1x+n1 y=m2x+n2

Então resolvi:

(-2K+2) . (-1) = -1

2k-2= -1

2k= 1

k = 1/2

Entretanto, aplicando-se a prova real, não se chega a um valor que coincida, também quero saber agora kkkk...

por Alysonaa Sex 02 Ago 2019, 01:06

Alysonaa escreveu:Resolvi a questão por geometria analítica, porém, o resultado foi 1/2, diferente do teu gabarito, claro.

Primeiramente, organizei as equações:

y(k-1)=x(-2k+2)-k

y(k-3)=-x+2k

Após isso, usei as relações das retas quanto suas posições, o que consiste em:

Perpendiculares: m1.m2= -1

Dado que:

y=m1x+n1 y=m2x+n2

Então resolvi:

(-2K+2) . (-1) = -1

2k-2= -1

2k= 1

k = 1/2

Entretanto, aplicando-se a prova real, não se chega a um valor que coincida, também quero saber agora kkkk...

Cara, fiz o seguinte, já que os valores acompanhando o x devem ser iguais

-2k+2= -1

-2k = -3

k= 3/2

Coincidem quando é feita a prova real

por **Emanuel Dias** Sex 02 Ago 2019, 01:10

Eu fiz assim:

(r): (2k-2)x+(k-1)y+k=0
(s): x+(k-3)y-2k=0

mr=\frac{-a}{b}=\frac{-(2k-2))}{k-1}

ms=\frac{-a}{b}=\frac{-1}{k-3}

Condição de perpendicularidade: mr=\frac{-1}{ms}

k-3=-\frac{(2k-2)}{k-1}

(k-1)(k-3)=2-2k

Essa equação tem delta 0 e admite somente 1 como raiz.

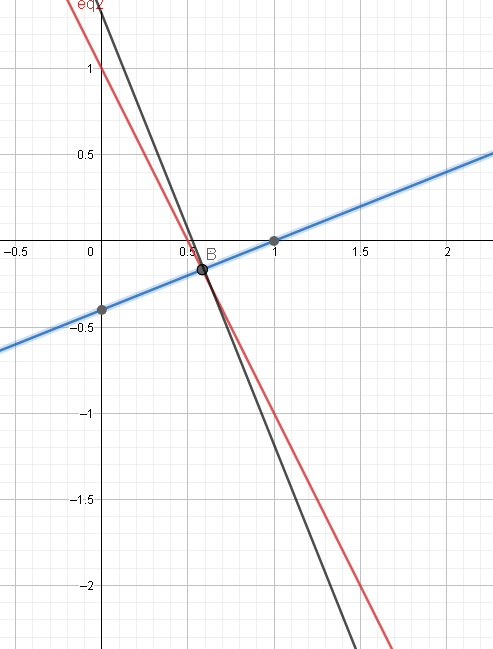
1/2 ta bem próximo de ser perpendicular

por **Emanuel Dias** Sex 02 Ago 2019, 01:13

Alysonaa escreveu:
Alysonaa escreveu:Resolvi a questão por geometria analítica, porém, o resultado foi 1/2, diferente do teu gabarito, claro.

Primeiramente, organizei as equações:

y(k-1)=x(-2k+2)-k

y(k-3)=-x+2k

Após isso, usei as relações das retas quanto suas posições, o que consiste em:

Perpendiculares: m1.m2= -1

Dado que:

y=m1x+n1 y=m2x+n2

Então resolvi:

(-2K+2) . (-1) = -1

2k-2= -1

2k= 1

k = 1/2

Entretanto, aplicando-se a prova real, não se chega a um valor que coincida, também quero saber agora kkkk...

Cara, fiz o seguinte, já que os valores acompanhando o x devem ser iguais

-2k+2= -1

-2k = -3

k= 3/2

Coincidem quando é feita a prova real

O modo que eu fiz que chega a resposta do gabarito, tem demonstração, deveria funcionar para todos os casos. Estranho Shocked

por **Medeiros** Sex 02 Ago 2019, 02:28

Tem erro nas equações das retas fornecidas.

k não pode ser 1, além de acarretar um absurdo, como alertou o colega Emanuel, também não gera solução para perpendicularidade.

Também não são solução os aventados valores de k = {5, 1/2, 3/2} porque não acarretam perpendicularidade.

por **Elcioschin** Sex 02 Ago 2019, 11:40

(2.k - 2).x + (k - 1).y + k = 0 ---> y = [- (2.k - 2)/(k - 1)].x - k/(k - 1) ---> m = - (2.k - 2)/(k - 1)

x + (k - 3).y - 2.k = 0 ---> y = [- 1/(k - 3)].x + 2.k/(k - 3) ---> m' = - 1/(k - 3)

m.m' = - 1 ---> [- (2.k - 2)/(k - 1)].[- 1/(k - 3)] = - 1 ---> [- (2.k - 2)/(k - 1)].[- 1/(k - 3)] + 1 = 0

(2.k - 2)/(k - 1).(k - 3) + 1 = 0 ---> [(2.k - 2) + (k - 1).(k - 3)]/(k - 1).(k - 3) = 0 --->

(2.k - 2 + k² - 4.k + 3)/(k - 1).(k - 3) = 0 ---> (k² - 2.k + 1)/(k - 1).(k - 3) = 0 --->

(k - 1)²/(k - 1).(k - 3) = 0 ---> (k - 1)/(k - 3) = 0 ---> k - 1 = 0 ---> k = 1