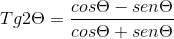Trigonometria
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1

Presa- Jedi

- Mensagens : 332
Data de inscrição : 02/03/2016
Idade : 26
Localização : Rio de Janeiro
 Re: Trigonometria
Re: Trigonometria
Usando prostaférese e os arcos complementares, temos no numerador de tan(2θ):cos(\theta)-sin(\theta)=sin(\frac{\pi}{2}-\theta)-sin(\theta)=2sin(\frac{\frac{\pi}{2}-\theta-\theta}{2})cos(\frac{\frac{\pi}{2}-\theta+\theta}{2})=2sin(\frac{\pi}{4}-\theta)cos(\frac{\pi}{4})=sin(\frac{\pi}{4}-\theta)\sqrt2
Faça o mesmo no denominador e obterácos(\frac{\pi}{4}-\theta)\sqrt2 . Portanto, a razão entre esses cancela o \sqrt2 e obtemos tan(2\theta)=tan(\frac{\pi}{4}-\theta) Como θ é angulo agudo (informação dada no enunciado), essa igualdade só e válida se os próprios ângulos das tangentes forem iguais: \frac{\pi}{4}-\theta=2\theta \Rightarrow \frac{\pi}{4}=3\theta Divida a igualdade por 3 e multiplique-a por 4: 4\theta=\frac{\pi}{3} \Rightarrow tan(4\theta)=tan(\frac{\pi}{3})=\sqrt3
Faça o mesmo no denominador e obterá
radium226- Recebeu o sabre de luz

- Mensagens : 117
Data de inscrição : 13/01/2019
Idade : 22
Localização : São Bernardo do Campo - SP
 Tópicos semelhantes
Tópicos semelhantes» [Resolvido] TRIGONOMETRIA Parte I: Ajuda para resolver questões de trigonometria
» TRIGONOMETRIA: Ajuda para resolver questões de trigonometria
» TRIGONOMETRIA: Ajuda para resolver questões de trigonometria
» trigonometria 5
» trigonometria
» TRIGONOMETRIA: Ajuda para resolver questões de trigonometria
» TRIGONOMETRIA: Ajuda para resolver questões de trigonometria
» trigonometria 5
» trigonometria
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos