Geometria plana - Teorema de Tales
Página 1 de 1
Geometria plana - Teorema de Tales
por Thiago@eam Sáb 18 maio 2019, 16:32
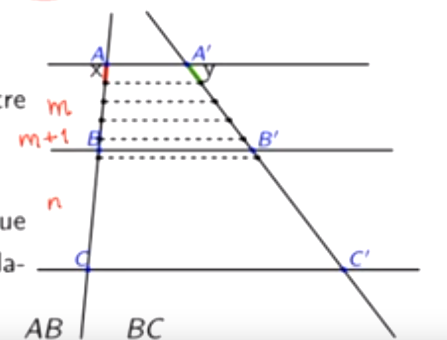
Sobre o teorema de Tales, (Se duas retas são transversais de um feixe de retas paralelas, então a razão entre dois segmentos quaisquer de uma delas é igual à razão entre os segmentos correspondentes da outra).
Considere AB e CD dois segmentos de uma transversal e A´B´ e C´D´ são os respectivos segmentos correspondentes da outra transversal.
Na demonstração do teorema para o caso em que AB e CD são incomensuráveis. BC = m*x ( x cabe m vezes em BC). por que dize-se que (m) < AB < (m+1)x
Não poderia ser m+2 ou qualquer outro número, ou mesmo AB > (m) ?
https://i.servimg.com/u/f51/20/07/20/33/captur11.png
Thiago@eam- Iniciante
- Mensagens : 44
Data de inscrição : 31/01/2019
Idade : 22
Localização : Maringá, Paraná Brasil
Tópicos semelhantes» Teorema de Tales - Geometria
» Provar teorema da geometria plana
» Geometria Plana - Teorema de Pitágoras
» Geometria Plana/Teorema dos Cossenos
» Teorema de Tales
» Provar teorema da geometria plana
» Geometria Plana - Teorema de Pitágoras
» Geometria Plana/Teorema dos Cossenos
» Teorema de Tales
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
