OBM nível 2
3 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
OBM nível 2
por Barbaducki Dom 12 maio 2019, 21:33
Numa lousa estão escritos inicialmente os números 1,2,...,10. Para quaisquer dois números a e b na lousa chamamos de S(a,b) a soma de todos os números na lousa com exceção de a e b. Uma operação permitida é escolher dois números a e b na lousa, apagá-Los e escrever o número a+b+(ab)/S(a,b). Após realizar essa operação algumas vezes restam na lousa apenas dois números x e y, com x maior ou igual a y.
a) Quantas operações foram realizadas?
b) Determine o maior valor possível para x.
Não conheço ninguém que havia matado essa.
a) Quantas operações foram realizadas?
b) Determine o maior valor possível para x.
Não conheço ninguém que havia matado essa.
Barbaducki- Recebeu o sabre de luz
- Mensagens : 119
Data de inscrição : 14/04/2019
Idade : 25
Localização : Rio de Janeiro
Re: OBM nível 2
por dd0123 Qua 16 Out 2019, 15:44
Olá, encontrei essa resolução: https://pt.quora.com/Como-posso-resolver-a-quest%C3%A3o-5-da-OBM-2018-Realmente-considero-como-a-mais-dif%C3%ADcil-da-prova
dd0123- Estrela Dourada
- Mensagens : 1362
Data de inscrição : 18/08/2018
Idade : 25
Localização : Brasil
Re: OBM nível 2
por NikolsLife Qui 02 Jan 2020, 17:38
Tomei um spoiler da solução enviada acima. Mas aqui está um caminho mais rápido:
a) 10-2 = 8 operações, pois todas as operações nos deixam com um número a menos.
b) S, a soma do produto dos pares de números em todos os pares é invariável, pois, quando a, b são apagados, perdemos ab + (a + b) S_ {a, b} e obtemos:
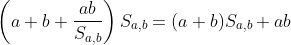
Então,
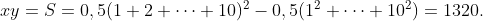
Além disso, observe que o mínimo nunca diminui, portanto y ≥ 1 ⇒ x ≤1320. A igualdade pode ser alcançada nunca usando 1 até que os únicos números restantes sejam 1, x ⇒ x = 1320.
a) 10-2 = 8 operações, pois todas as operações nos deixam com um número a menos.
b) S, a soma do produto dos pares de números em todos os pares é invariável, pois, quando a, b são apagados, perdemos ab + (a + b) S_ {a, b} e obtemos:
Então,
Além disso, observe que o mínimo nunca diminui, portanto y ≥ 1 ⇒ x ≤1320. A igualdade pode ser alcançada nunca usando 1 até que os únicos números restantes sejam 1, x ⇒ x = 1320.
NikolsLife- Padawan
- Mensagens : 84
Data de inscrição : 10/12/2019
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
