Inequação Modular
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Inequação Modular
por Infantes Sex 26 Abr 2019, 20:39
(EN) Se M = { |x² + x| ≤ |x + 1| então M é:
Resposta
[-1,1]
O que há de errado no meu procedimento, ou melhor: O que há de certo?
Resposta
[-1,1]
O que há de errado no meu procedimento, ou melhor: O que há de certo?
Infantes- Recebeu o sabre de luz
- Mensagens : 144
Data de inscrição : 03/03/2019
Re: Inequação Modular
por Vitor Ahcor Sex 26 Abr 2019, 20:54
Olá,
Acredito que você fez alguns cálculos que não eram necessários, veja:
|x² + x| ≤ |x + 1|
|x|*|x + 1| ≤ |x + 1|
1° Caso: x ≠ -1
|x| ≤ 1 --> -1 ≤ x ≤ 1
2° Caso: x = -1
|-1|*|-1 + 1| ≤ |-1 + 1| Ok!
Daí, x ∈ [-1,1]
Acredito que você fez alguns cálculos que não eram necessários, veja:
|x² + x| ≤ |x + 1|
|x|*|x + 1| ≤ |x + 1|
1° Caso: x ≠ -1
|x| ≤ 1 --> -1 ≤ x ≤ 1
2° Caso: x = -1
|-1|*|-1 + 1| ≤ |-1 + 1| Ok!
Daí, x ∈ [-1,1]
____________________________________________
Cha-la head-cha-la
Vitor Ahcor- Monitor
- Mensagens : 780
Data de inscrição : 21/12/2018
Idade : 24
Localização : Taurdal
Re: Inequação Modular
por Jessie Sex 26 Abr 2019, 23:35
Você checou as restrições mas não aplicou e esqueceu do sinal "-" que havia antes de \left |x + 1 \right | quando foi retirar os módulos.
\left |x^2 + x \right | \leq \left |x + 1 \right |
\left |x^2 + x \right | - \left |x + 1 \right | \leq 0
I) Sex\geq 0
(x^2 + x ) - (x + 1) \leq 0
II) Se -1 < x < 0
-(x^2 + x )- (x + 1) \leq 0
III) Se x < -1
x^2 + x - (-x - 1) \leq 0
IV) Se x = -1
-(x^2 + x )- (x + 1) \leq 0
\left |x^2 + x \right | \leq \left |x + 1 \right |
\left |x^2 + x \right | - \left |x + 1 \right | \leq 0
I) Se
(x^2 + x ) - (x + 1) \leq 0
II) Se
-(x^2 + x )- (x + 1) \leq 0
III) Se
x^2 + x - (-x - 1) \leq 0
IV) Se x = -1
-(x^2 + x )- (x + 1) \leq 0
Jessie- Recebeu o sabre de luz
- Mensagens : 181
Data de inscrição : 29/11/2017
Idade : 42
Localização : Guarulhos - SP
Re: Inequação Modular
por Infantes Sáb 27 Abr 2019, 16:09
Jessie, não esqueci do sinal, tanto é que fiz de novo aqui e acabo por não chegar em nada. Segue em anexo
Infantes- Recebeu o sabre de luz
- Mensagens : 144
Data de inscrição : 03/03/2019
Re: Inequação Modular
por Jessie Sáb 27 Abr 2019, 22:56
Você está aplicando errado as restrições, como admitir na sua primeira conclusão (1) que quando x ≤ - 1 o valor do que está dentro de |x + 1| é negativo, mas é negativo apenas para x < -1 e também na sua última resposta acrescentou o valor de 1 nas restrições por algum motivo que desconheço.
Faça uma comparação:
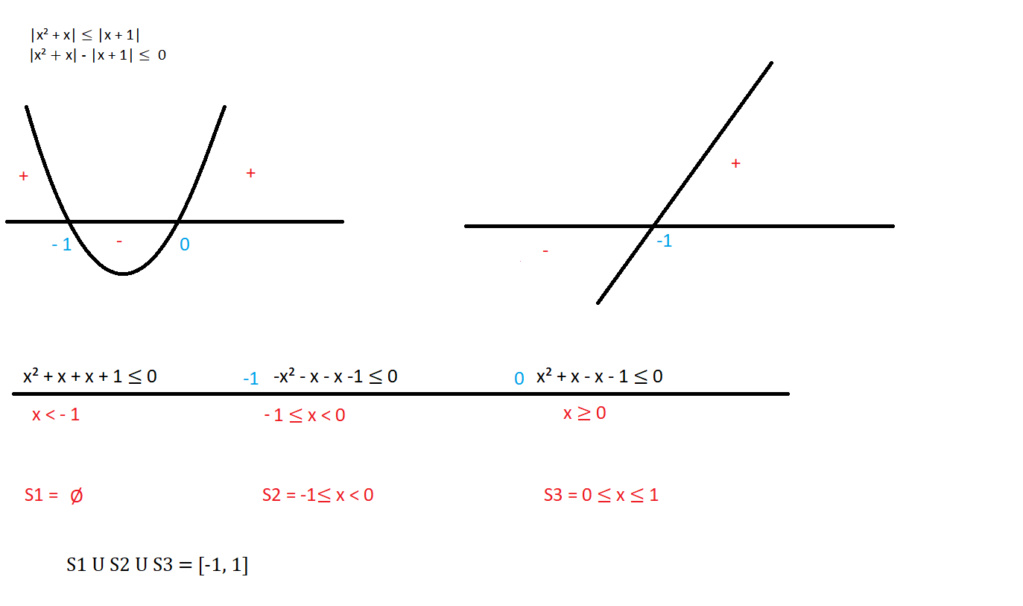
Faça uma comparação:
Jessie- Recebeu o sabre de luz
- Mensagens : 181
Data de inscrição : 29/11/2017
Idade : 42
Localização : Guarulhos - SP
Tópicos semelhantesPiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
