Inequação Modular

por Kelvin Brayan Qua 14 Set - 12:21

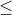(UFF-RJ) Com relação aos conjuntos P = {x e Z| |x| é $\leq \sqrt[]{7}$ } e Q = { x e Z | x² $\leq$ 0,333...}, afirma-se:
I. P U Q = P
II. Q - P = {0}
III. P C Q
IV. P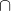 $\cap$ Q = Q
Somente são verdadeiras as afirmativas
A) I e III
B) I e IV
C) II e III
D) II e IV
E) III e IV

Tentativa:
Conjunto P
$-\sqrt[]{7}\leq x \leq \sqrt{7} \simeq - 2,65 \leq x \leq 2,65$

Conjunto Q
$-0,333... \leq x^{2} \leq 0,333...$
Então, como eu vou fazer raiz quadrada de -0,333... ? Não existe no conjunto dos inteiros nem dos reais. Eu até acertei essa questão, mas queria saber o que devo fazer nesse último caso!!!

por **abelardo** Qua 14 Set - 13:19

Veja que 0,333... é uma dízima periódica, podemos transformá-la numa fração.

$0,333...=\frac{1}{3}$

Você pode, como uma de várias técnicas, transformar a desigualdade numa inequação do segundo grau.

$x^2<\frac{1}{3}$

$x^2-\frac{1}{3}<0$

Uma solução aproximada é $-0,5<x<0,5$ .

Você poderia fazer simples ''testes'', já que os conjuntos soluções são números inteiros. Veja que:
$\left\{\begin{matrix} 0^2=0\\ 1^2=(-1)^2=1\\ 2^2=(-2)^2=4 \end{matrix}\right.$

Verá que zero é o único inteiro que satisfaz a condição para os elementos do conjunto Q.

por Kelvin Brayan Qua 14 Set - 13:59

Hun... entendi!

Valeu!

por Conteúdo patrocinado

Inequação Modular

Inequação Modular

Re: Inequação Modular

Re: Inequação Modular

Re: Inequação Modular

Um fórum livre e democrático.