secante
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
secante
por Omagodasexatas3,14 Sex 12 Abr 2019, 17:01
Calcule m de modo que :
sec(
) = 
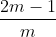, com 
]
,
]
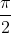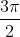Resposta: {m
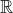| 0
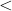m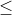
}
Se alguém puder me ajudar na resolução do exercício fico agradecido,forte abraço!
sec(
Resposta: {m
Se alguém puder me ajudar na resolução do exercício fico agradecido,forte abraço!
Omagodasexatas3,14- Recebeu o sabre de luz
- Mensagens : 111
Data de inscrição : 07/09/2017
Idade : 28
Localização : São Paulo, São paulo, Brasil
Re: secante
por Elcioschin Sex 12 Abr 2019, 17:30
secα = 1/cosα
No 2º e 3º quadrantes ---> cosα < 0 ---> secα < 0
Para α = pi ---> cos(pi) = - 1 ---> sec(pi) = - 1
sec(pi) = (2.m - 1)/m ---> - 1 = (2.m - 1)/m ---> m = 1/3
Complete, lembrando que secα ≤ -1 e secα ≥ 1
No 2º e 3º quadrantes ---> cosα < 0 ---> secα < 0
Para α = pi ---> cos(pi) = - 1 ---> sec(pi) = - 1
sec(pi) = (2.m - 1)/m ---> - 1 = (2.m - 1)/m ---> m = 1/3
Complete, lembrando que secα ≤ -1 e secα ≥ 1
Elcioschin- Grande Mestre
- Mensagens : 73174
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
secante
por Omagodasexatas3,14 Ter 23 Abr 2019, 11:25
elcio, eu não consegui completar ... me ajude por favor.
Omagodasexatas3,14- Recebeu o sabre de luz
- Mensagens : 111
Data de inscrição : 07/09/2017
Idade : 28
Localização : São Paulo, São paulo, Brasil
Re: secante
por Elcioschin Ter 23 Abr 2019, 11:57
A primeira coisa é lembrar que o denominador não pode ser nulo: m ≠ 0
Sabemos também que secα ≤ - 1 e secα ≥ 1
Como o ângulo está no 2º ou 3º quadrantes ---> secα ≤ - 1
Já aprovado que m = 1/3
Basta testar valores m < 1/3 (por exemplo m = -1), m > 1/3 (por exemplo m = 2/3) e 0 < m < 1/3 (por exemplo m = 1/4) e ver qual deles atende
Sabemos também que secα ≤ - 1 e secα ≥ 1
Como o ângulo está no 2º ou 3º quadrantes ---> secα ≤ - 1
Já aprovado que m = 1/3
Basta testar valores m < 1/3 (por exemplo m = -1), m > 1/3 (por exemplo m = 2/3) e 0 < m < 1/3 (por exemplo m = 1/4) e ver qual deles atende
Elcioschin- Grande Mestre
- Mensagens : 73174
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
