A soma dos números associados aos itens verdadeiros é um número do intervalo

Na reta real abaixo estão representados os números reais a, b, c, d, zero e 1.



Analise os itens abaixo, classificando-os em (V) verdadeiros ou (F) falsos.

(01)
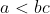
(03)
(04)
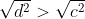
(06)
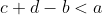
(08)

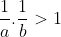
A soma dos números associados aos itens verdadeiros é um número do intervalo


a)[1, 5] c)[18, 22]
b)[6, 11] d)[12, 17]

Analisemos uma por vez:

(01) a < b*c

a e b são positivos, porém c é negativo. O produto b*c resulta em um número negativo; como a é positivo, a > b*c.

Afirmativa falsa

(03) 0 < a*b < 1

a e b são positivos maiores que 0 e menores que 1; seu produto resultará sempre em um número compreendido entre 0 e 1.

Afirmativa verdadeira

(04) \/d² > \/c²
d e c são negativos, porém d tem módulo maior que c. Como elevando ao quadrado o número se torna positivo, é fato que \/d² > \/c². Note que d < c, se não usarmos módulo.

Afirmativa verdadeira

(06) c + d - b < a

Você está somando duas parcelas estritamente negativas (c e d) com uma só parcela positiva (b). O resultado será negativo e garante que seja menor que a.

Afirmativa verdadeira

(08) 1/a * 1/b > 1

Como a e b estão entre 0 e 1, são números decimais. A divisão de números positivos por números decimais será sempre um número maior que 1. Exemplo: considere se b fosse 0,5. 1/b = 1/0,5 = 2; e a = 0,9. 1/a = 1/9 = 1,111... Seu produto daria 2,222..., que é maior que 1.

Afirmativa verdadeira

Soma das corretas: 3 + 4 + 6 + 8 = 21
Alternativa C

Se não errei é isso, caso tenha errado avisem.

Abraços

Está correta , olhei no gabarito e deu letra c
muito obrigado

Drufox escreveu:Está correta , olhei no gabarito e deu letra c
muito obrigado

Beleza Drufox mas lembre-se de que quando postar a questão postar também o gabarito! Ajuda muito! Abraços