Triângulo equilátero e hexágono inscritos

Boa noite

Será que vocês poderiam gentilmente me ajudar com esta questão?

- Em uma circunferência estão inscritos um triângulo eqüilátero e um hexágono regular. O apótema do triângulo somado com o apótema do hexágono dá 12(raiz(3) + 1) cm. O lado do triângulo, em cm, mede 

a) 12 raiz(3)
b) 16 raiz(3)
c) 20 raiz(3)
d) 24 raiz(3)

Estou retomando meus estudos, mas a situação está complicada. Tentei fazer apótema do triângulo = 1/3 do raio e apótema do hexágono = raio . raiz(3) / 2, mas só estou levando pau.

Se puderem ajudar com bastante detalhe, ficarei muito grato

Obrigado

Seja R o raio do círculo

L₃ = 2.R.cos30º ---> L₃ = 2.R.(√3/2) ---> L₃ = R.√3 ---> I

At = (1/3).(L₃.cos30º) ---> At = (1/3).(R.√3).(√3/2) ---> At = R/2 ---> II


L₆ = R

Ah = R.cos30º ---> Ah = R.√3/2 ---> III

III + II ---> Ah + At = R.√3/2 + R/2 ---> Ah + At = (R/2).(√3 + 1)

R/2 = 12 ---> R = 24

I) L₃ = 24.√3

Elcioschin escreveu:Seja R o raio do círculo

L₃ = 2.R.cos30º ---> L₃ = 2.R.(√3/2) ---> L₃ = R.√3 ---> I

At = (1/3).(L₃.cos30º) ---> At = (1/3).(R.√3).(√3/2) ---> At = R/2 ---> II


L₆ = R

Ah = R.cos30º ---> Ah = R.√3/2 ---> III

III + II ---> Ah + At = R.√3/2 + R/2 ---> Ah + At = (R/2).(√3 + 1)

R/2 = 12 ---> R = 24

I) L₃ = 24.√3

Obrigado, Elcio!!

Não entendi esta parte:

At = (1/3).(L3.cos30º) ---> At = (1/3).(R.√3).(√3/2) ---> At = R/2 ---> II

Eu fiz por pitágoras e achei o resultado igual, mas queria saber como vc fez. Será que vc poderia me explicar com mais detalhes essa parte?

Saudades do Euclides. Fico feliz que vc continua com a gente!

Forte abraço

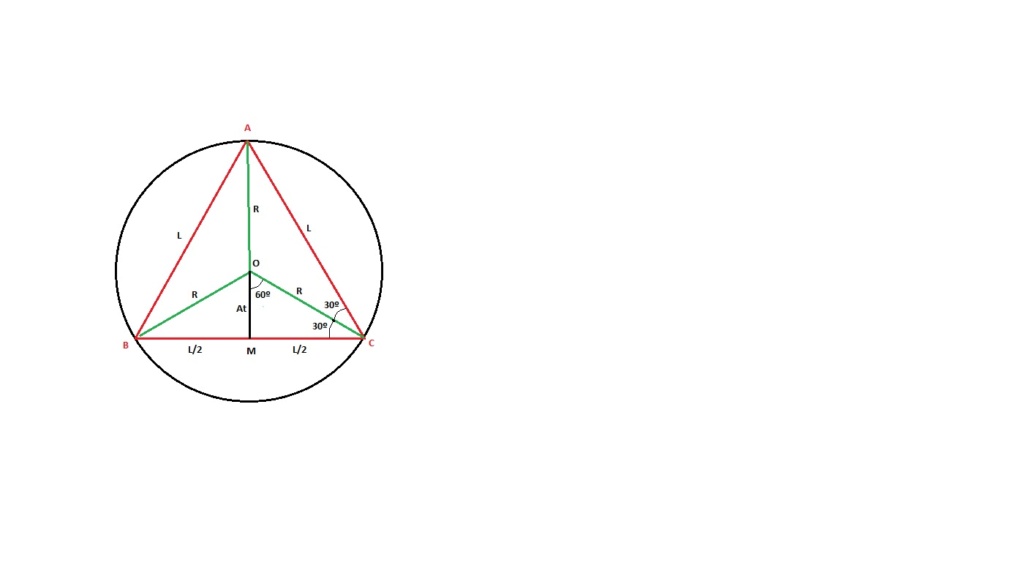
Desenhe um círculo de centro O e raio R e inscreva nele um triângulo equilátero ABC

Trace OA, OB e OC ---> OA = OB = OC = R

BÂC = A^CB = C^AB = 60º ---> OÂB = O^BA = OÂC = O^CA = O^CB = O^BC 30º --->

Seja M o ponto médio de AB ---> trace COM ---> COM é perpendicular a AB

No triângulo retângulo AMC ---> AC = L₃

CM = AC.cos(OÂC) ---> CM = L₃.cos30º

CM é mediana relativa a AB ---> OC = 2.OM

OM + OC = CM ---> OM + 2.OM = CM ---> 3.OM = CM ---> OM = (1/3).CM ---> At = (1/3).(L₃.cos30º)

Consegui entender a lógica, Elcio! Muito obrigado!

Forte abraço!

Uma solução bem mais rápida (com trigonometria do triângulo retângulo):

OM = OC.cos(AÔC) ---> A_t = R.cos60º ---> A_t = R.(1/2) ---> A_t = = R/2