Quadrado e hexagono inscritos.

Em uma circunferencia de centro O e raio 2 tem-se duas cordas paralelas AB e CD,lados do quadrado e do hexágono regular convexos inscritos,respectivamente.A distancia EF entre essas cordas é aproximadamente igual a:
a)√5
b) μ
c)√6
d)2
e)μ/2

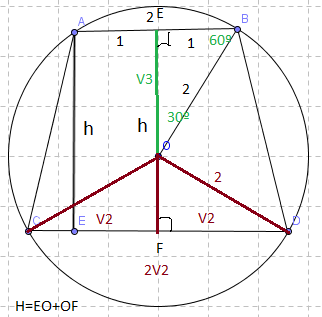
Lembre que:
O lado do hexágono regular inscrito é igual ao raio, e o lado do quadrado inscrito é igual ao raio vezes V2.
Tente concluir:
Calcule OF aplicando Pitágoras no triângulo FOD, depois some OF+V3.
Se não consegui diga que concluiremos. Boa Noite

att

att

Nao entendi muito bem a figura,os triangulos formados nao sao equilateros?o que seria esse v2 e v3?poderia fazer pra mim?

Desenhe um hexágono regular inscrito num círculo e ligue seus vértices ao centro do círculo.
Perceba que ficaram formados 6 triângulos equiláteros . Trace a altura de um desses triângulos e veja que ficaram formados dois triângulos retângulos com ângulos de 30,60 e 90°. Na nossa figura triângulo BOE. É sabido que em todo triângulo retângulo 30,60 e 90 o menor cateto mede a metade da hipotenusa e o maior mede o menor vezes V3 . Nosso triângulo BOE a hipotenusa OB= raio=2 , então o menor cateto mede 1 e o maior mede 1.V3.

Agora desenhe um quadrado inscrito em um círculo. Ligue as duas diagonais desse quadrado, perceba que a diagonal corresponde a 2R , mais a diagonal do quadrado inscrito mede D=LV2---> 2R=LV2--->2.2=LV2-->L=4/V2=4V2/2=2V2

att