Equação trigonométrica

por marcosprb Ter 12 Fev 2019, 14:05

Ainda estou com dúvidas em relação a esse tipo de equação
Resolva a equação
$tg\left ( 3x+\frac{\pi}{6} \right )=-\frac{\sqrt{3}}{3}$

No universo U= [0;2pi]

Gabarito:
$\frac{2\pi}{9};\frac{5\pi}{9};\frac{8\pi}{9};\frac{11\pi}{9};\frac{14\pi}{9};\frac{17\pi}{9};$

por **Giovana Martins** Ter 12 Fev 2019, 14:19

\\tg(\alpha )=tg(\beta )\to \alpha =\beta +k\pi\\\\tg\left ( 3x+\frac{\pi }{6} \right )=-\frac{\sqrt{3}}{3}\to tg\left ( 3x+\frac{\pi }{6} \right )=tg\left ( \frac{5\pi }{6} \right )\\\\3x+\frac{\pi }{6}= \frac{5\pi }{6}+k\pi \to x=\frac{2\pi }{9}+\frac{k\pi }{3},k\in \mathbb{Z}

por marcosprb Ter 12 Fev 2019, 14:45

Bem, o que eu fiz(e que confere com o gabarito) foi o seguinte:
Para o universo [0;2pi]:
$x= tg\left (- \frac{\sqrt{3}}{3} \right ) => x=\frac{5\pi}{6};\frac{11\pi}{6}$

Então:
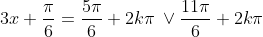
$3x+\frac{\pi}{6}=\frac{5\pi}{6}+2k\pi \: \vee \frac{11\pi}{6}+2k\pi$

Portanto:

$x=\frac{2\pi}{9}+\frac{2k\pi}{3}\: \vee \: \frac{5\pi}{9}+\frac{2k\pi}{3}, k=(0,1,2)$

Substituindo os valores de k para 0,1,2 eu encontro as respostas do gabarito.

Minha dúvida é: (No intervalo de [0;2pi]
Por exemplo, se tgx=1 ==> x=pi/4 ou x=5pi/4
Mas se tg3x=1 => Existem 6 valores que satisfazem essa equação
que seriam: x=pi/12+2kpi/3 ou 5pi/12 +2kpi/3, com k podendo ser 0,1,2

O que não ficou intuitivo pra mim é ter que adicionar esse 2kpi/3 e ter que substituir os valores de k para achar as respostas.

por marcosprb Ter 12 Fev 2019, 14:56

Giovana Martins escreveu:
\\tg(\alpha )=tg(\beta )\to \alpha =\beta +k\pi\\\\tg\left ( 3x+\frac{\pi }{6} \right )=-\frac{\sqrt{3}}{3}\to tg\left ( 3x+\frac{\pi }{6} \right )=tg\left ( \frac{5\pi }{6} \right )\\\\3x+\frac{\pi }{6}= \frac{5\pi }{6}+k\pi \to x=\frac{2\pi }{9}+\frac{k\pi }{3},k\in \mathbb{Z}

Essa resposta pertence ao domínio da função? E se k for um valor tal que $\frac{2\pi}{9}+\frac{k\pi}{3}$ seja maior que 2pi ?

por **Giovana Martins** Ter 12 Fev 2019, 15:18

"Minha dúvida é: (No intervalo de [0;2pi]
Por exemplo, se tgx=1 ==> x=pi/4 ou x=5pi/4
Mas se tg3x=1 => Existem 6 valores que satisfazem essa equação
que seriam: x=pi/12+2kpi/3 ou 5pi/12 +2kpi/3, com k podendo ser 0,1,2"

Marcos, nesta parte, eu honestamente não entendi a sua dúvida.

"O que não ficou intuitivo pra mim é ter que adicionar esse 2kpi/3 e ter que substituir os valores de k para achar as respostas."

Do jeito que você desenvolveu o seu raciocínio aparentemente está correto (as suas soluções gerais pegaram todos os arcos que são soluções), embora para mim me soe estranha a representação dos arcos que são solução como se eles fosse obtidos a cada volta no ciclo (isso ficou indicado quando você somou 2kpi), pois os arcos côngruos a 5pi/6 e 11pi/6 são obtidos a cada meia volta (kpi).

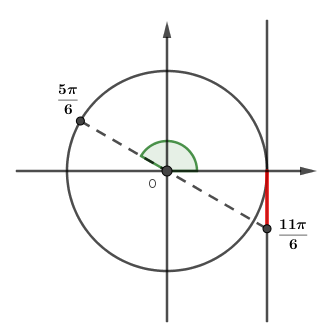
Para a sua terceira dúvida: a resposta que eu cheguei é uma solução geral, ou seja, se o seu enunciado não delimitasse um intervalo, [0,2pi], a forma das soluções da equação seria o 2pi/9+kpi/3. No intervalo dado pela questão, ao tomarmos um valor para k tal que x não pertença ao intervalo [0,2pi], então concluímos que esse x não é solução.

por **Giovana Martins** Ter 12 Fev 2019, 15:29

Outra coisa que eu esqueci de dizer: equações trigonométricas tem um roteiro básico de resolução.

1°) encontrar as soluções gerais
2°) atribuir valores para k para encontrar os arcos que são soluções da equação.

Quando você atribui valores para k você encontra todos os arcos côngruos, por exemplo, de 2pi/9, que são soluções da equação por pertencerem ao intervalo dado pelo enunciado.

Se o enunciado não estabelecer um intervalo então as soluções são as soluções gerais, a+kpi ou a+2kpi, onde a corresponde "a" corresponde ao ângulo na primeira volta (ou meia volta) e kpi ou 2kpi representa os arcos côngruos a "a" nas demais voltas.

por marcosprb Ter 12 Fev 2019, 15:38

Me desculpe, não consegui expressar bem a minha dúvida, mas creio que seja parecida com o que você disse em [...]''embora para mim me soe estranha a representação dos arcos que são solução como se eles fosse obtidos a cada volta no ciclo (isso ficou indicado quando você somou 2kpi)''

Veja essa questão que eu postei: https://pir2.forumeiros.com/t156600-equacao-trigonometrica

----------------------

''a resposta que eu cheguei é uma solução geral, ou seja, se o seu enunciado não delimitasse um intervalo, [0,2pi], a forma das soluções da equação seria o 2pi/9+kpi/3. No intervalo dado pela questão, ao tomarmos um valor para k tal que x não pertença ao intervalo [0,2pi], então concluímos que esse x não é solução.''

Sobre isso, o meu livro também trouxe uma questão igual a essa mas com intervalo nos reais, e o gabarito é o seguinte:
$S=\left ( x \in \mathbb{R}| x=\frac{-\pi}{9}+\frac{2k\pi}{3}, x \in \mathbb{Z} \right )$

por marcosprb Ter 12 Fev 2019, 15:44

Giovana Martins escreveu:
Outra coisa que eu esqueci de dizer: equações trigonométricas tem um roteiro básico de resolução.

1°) encontrar as soluções gerais
2°) atribuir valores para k para encontrar os arcos que são soluções da equação.

Quando você atribui valores para k você encontra todos os arcos côngruos, por exemplo, de 2pi/9, que são soluções da equação por pertencerem ao intervalo dado pelo enunciado.

Se o enunciado não estabelecer um intervalo então as soluções são as soluções gerais, a+kpi ou a+2kpi, onde a corresponde "a" corresponde ao ângulo na primeira volta (ou meia volta) e kpi ou 2kpi representa os arcos côngruos a "a" nas demais voltas.

Acredito que nessa questão o autor atribuiu o valor de ''a'' como sendo -pi/3, pelo fato de
$arctg\left (- \frac{\sqrt{3}}{3} \right )=-\frac{\pi}{6}$

Eu optei por pegar o 5pi/6 para no final eu não ter que encontrar a primeira determinação positiva para enquadrar a solução no intervalo dado (em alguns casos é necessário quando se pega o arco no sentido horário.) e também porque eu prefiro trabalhar com arcos no sentido tradicional de se percorrer o ciclo trigonométrico.

por marcosprb Ter 12 Fev 2019, 15:54

Quando você diz que ''a'' corresponde ao ângulo na primeira volta, tanto faz o sentido ser horário ou anti-horário ?

por **Giovana Martins** Ter 12 Fev 2019, 15:56

"Veja essa questão que eu postei: https://pir2.forumeiros.com/t156600-equacao-trigonometrica"

Ah sim, mas essa questão diferencia um pouquinho as coisas.

Nas literaturas que eu tive contato, em equações em tangente, os arcos que são soluções dessas equações são da forma a=b+kpi.

Em cosseno: a=±b+2kpi (neste caso podemos ter kpi também, por exemplo, para o caso em que tem-se cos(x)=0, em que pi/2+kpi é solução, tendo em vista que x=3pi/2 também é solução e dista pi de pi/2 e assim por diante para os próximos arcos côngruos.)

Em seno: a=b+2kpi ou a=pi-b+2kpi (também podendo variar entre kpi e 2kpi).

Esses são os modelos de soluções gerais que eu tive contato. Só por isso eu estranhei.

Quanto a outra citação. Também está correto aquele arco. Para testar basta tomar valores de k tal que x pertença ao intervalo [0,2pi] (como contraexemplo).