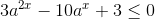Inequação exponencial
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Inequação exponencial
por marcosprb Qua Fev 06 2019, 20:47
Sendo a um número real positivo e diferente de 1, resolva a inequação:
Última edição por marcosprb em Qua Fev 06 2019, 21:59, editado 1 vez(es)
marcosprb- Mestre Jedi
- Mensagens : 825
Data de inscrição : 08/05/2017
Re: Inequação exponencial
por Vitor Ahcor Qua Fev 06 2019, 21:26
Olá!
(*) a^x = y
(**) 3y^2 -10y + 3 ≤ 0
(y-3)*(3y-1) ≤ 0
.: 1/3 ≤ y ≤ 3
(i) Para a > 1:
1/3 ≤ a^x ≤ 3
-log_a (3) ≤ x ≤ log_a (3)
(ii) Para 0 < a < 1 :
1/3 ≤ a^x ≤ 3
log_a(3) ≤ x ≤ -log_a(3)
(*) a^x = y
(**) 3y^2 -10y + 3 ≤ 0
(y-3)*(3y-1) ≤ 0
.: 1/3 ≤ y ≤ 3
(i) Para a > 1:
1/3 ≤ a^x ≤ 3
-log_a (3) ≤ x ≤ log_a (3)
(ii) Para 0 < a < 1 :
1/3 ≤ a^x ≤ 3
log_a(3) ≤ x ≤ -log_a(3)
____________________________________________
Cha-la head-cha-la
Vitor Ahcor- Monitor
- Mensagens : 780
Data de inscrição : 21/12/2018
Idade : 24
Localização : Taurdal
Re: Inequação exponencial
por marcosprb Qua Fev 06 2019, 22:00
Obrigado!vitorrochap2013 escreveu:Olá!
(*) a^x = y
(**) 3y^2 -10y + 3 ≤ 0
(y-3)*(3y-1) ≤ 0
.: 1/3 ≤ y ≤ 3
(i) Para a > 1:
1/3 ≤ a^x ≤ 3
-log_a (3) ≤ x ≤ log_a (3)
(ii) Para 0 < a < 1 :
1/3 ≤ a^x ≤ 3
log_a(3) ≤ x ≤ -log_a(3)
marcosprb- Mestre Jedi
- Mensagens : 825
Data de inscrição : 08/05/2017
Tópicos semelhantesPiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
