(ITA-2005)Módulo
4 participantes
Página 1 de 1
 (ITA-2005)Módulo
(ITA-2005)Módulo
Determine todos os valores reais de a para os quais a equação 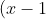^2=\left | x-a \right |) admita exatamente três soluções distintas.
admita exatamente três soluções distintas.
Sei que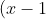^2\geq 0)
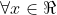 . Por definição,
. Por definição, ^2\\ -(x-1)^2 \end{matrix}\right.) . Desenvolvi os dois produtos notáveis e isolei a em cada equações para depois igualar as duas equações..
. Desenvolvi os dois produtos notáveis e isolei a em cada equações para depois igualar as duas equações..
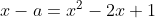 -->
--> 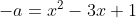
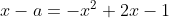 -->
--> 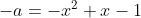
Igualando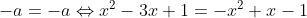 ,
,
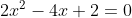 e encontrei 1 como única raiz para a equação. Substituindo encontro 1 para o valor de a...
e encontrei 1 como única raiz para a equação. Substituindo encontro 1 para o valor de a...
Sei que está errado e não tenho gabarito.. alguém socorre?
Sei que
Igualando
Sei que está errado e não tenho gabarito.. alguém socorre?

abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
 Re: (ITA-2005)Módulo
Re: (ITA-2005)Módulo
Olá Abelardo,
É melhor vc tentar fazer os gráficos e ver aonde ocorre tangencia para x < a e x > a. Essa questão é facilmente resolvida dessa forma:
(x - 1)² = |x - a|
Delta = 0 ---> para ocorrer a tangência
i) x² - 2x + 1 = x - a
x² - 3x + (1 + a) = 0
Delta: 9 - 4 - 4a = 0
5 - 4a = 0
4a = 5
a = 5/4
ii) -x² + 2x - 1 = x - a
-x² + x - 1 + a = 0
Delta: 1 - 4*-1(-1 + a) = 0
1 - 4 + 4a = 0
4a = 3
a = 3/4
iii) É exatamente a que vc fez a = 1 e x = 1
Os valores de a são {5/4,3/4,1}
É melhor vc tentar fazer os gráficos e ver aonde ocorre tangencia para x < a e x > a. Essa questão é facilmente resolvida dessa forma:
(x - 1)² = |x - a|
Delta = 0 ---> para ocorrer a tangência
i) x² - 2x + 1 = x - a
x² - 3x + (1 + a) = 0
Delta: 9 - 4 - 4a = 0
5 - 4a = 0
4a = 5
a = 5/4
ii) -x² + 2x - 1 = x - a
-x² + x - 1 + a = 0
Delta: 1 - 4*-1(-1 + a) = 0
1 - 4 + 4a = 0
4a = 3
a = 3/4
iii) É exatamente a que vc fez a = 1 e x = 1
Os valores de a são {5/4,3/4,1}
 Re: (ITA-2005)Módulo
Re: (ITA-2005)Módulo
Já tava digitando a resposta em LaTeX, ai vi que você respondeu, mas é isso ai mesmo que eu encontrei.

Matheus Basílio- Elite Jedi

- Mensagens : 344
Data de inscrição : 22/10/2010
Idade : 28
Localização : Palmas, Tocantins
 Re: (ITA-2005)Módulo
Re: (ITA-2005)Módulo
Desculpe-me Luiseduardo por desenterrar essa questão, mas porque você disse que para ocorrer tangência, delta deve ser igual a zero?

abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
 Re: (ITA-2005)Módulo
Re: (ITA-2005)Módulo
A interseção da parábola com equação modular ocorrer em apenas um ponto (uma solução).
Espero que te ajude e seja isso.
Espero que te ajude e seja isso.
hygorvv- Elite Jedi

- Mensagens : 1721
Data de inscrição : 15/03/2010
Idade : 35
Localização : Vila Velha
 Re: (ITA-2005)Módulo
Re: (ITA-2005)Módulo
Agora sim pude entender. Essa equação modular é bem simples e sua representação no plano cartesiano são duas retas que ''partem'' do eixo das abscissas. A única forma de termos três soluções para igualdade dada é a parábola tocar também o eixo das abscissas e delta, então, será igual a zero. Obrigado Hygorvv, Matheus Basílio e Luis Eduardo.

abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Módulo FGV 2005
» Inequação Modular (Módulo em Módulo)
» Inequação de um módulo de módulo
» Módulo dentro de módulo
» CM-2005
» Inequação Modular (Módulo em Módulo)
» Inequação de um módulo de módulo
» Módulo dentro de módulo
» CM-2005
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













