Demonstração de soma de arcos (Trigonometria)
2 participantes
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
Demonstração de soma de arcos (Trigonometria)
por W_Yuri Seg 14 Jan 2019, 19:11
Adição e Subtração de arcos
As fórmulas são:
sen(α±β)= senα.cosβ ± senβ.cosα
cos(α±β)= cosα.cosβ ∓ senα.senβ
tan(α±β)= tanα ± tanβ/1 ∓ tanα.tanβ
Demonstração:
Inicialmente, sobrepomos um triângulo retângulo de ângulo α a um de ângulo β e hipotenusa 1 como na figura:
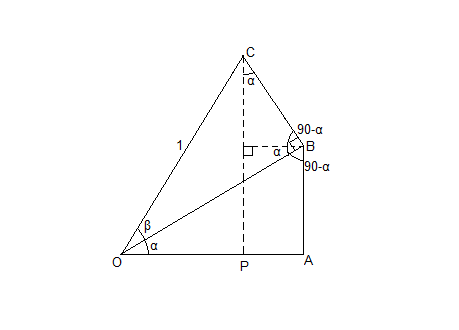
Em seguida, pensemos no seno como a projeção da hipotenusa no cateto para o qual o ângulo olha, e o cosseno como a projeção no cateto colado ao ângulo.
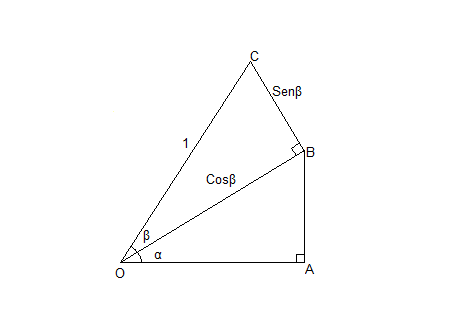
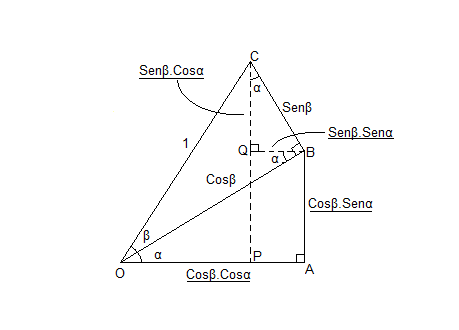
No triângulo OBC, temos: OB=Cosβ e BC=Senβ.
No triângulo OAB, temos: OA=Cosα.hipotenusa = Cosα.Cosβ e AB=Senα.Cosβ.
No triângulo QBC, temos: BQ=hipotenusa.Senα = Senβ.Senα e QC=Senβ.Cosα.
Olhando agora para o triângulo OPC, temos:
Sen(α+β)= PC/1 = AB+QC = Senα.Cosβ + Senβ.Cosα
Cos(α+β)= PO/1 = OA-BQ = Cosα.Cosβ - Senα.Senβ
Para a Tangente, dividimos uma pela outra:
Tan(α+β)= Sen(α+β)/Cos(α+β) = Senα.Cosβ + Senβ.Cosα/Cosα.Cosβ - Senα.Senβ (Dividindo em cima e embaixo por Cosα.Cosβ)
Tan(α+β)= tanα+tanβ/1∓ tanα.tanβ
Para as de subtração, escrevemos α-β = α+ (-β) e usamos paridade.
As fórmulas são:
sen(α±β)= senα.cosβ ± senβ.cosα
cos(α±β)= cosα.cosβ ∓ senα.senβ
tan(α±β)= tanα ± tanβ/1 ∓ tanα.tanβ
Demonstração:
Inicialmente, sobrepomos um triângulo retângulo de ângulo α a um de ângulo β e hipotenusa 1 como na figura:
Em seguida, pensemos no seno como a projeção da hipotenusa no cateto para o qual o ângulo olha, e o cosseno como a projeção no cateto colado ao ângulo.
No triângulo OBC, temos: OB=Cosβ e BC=Senβ.
No triângulo OAB, temos: OA=Cosα.hipotenusa = Cosα.Cosβ e AB=Senα.Cosβ.
No triângulo QBC, temos: BQ=hipotenusa.Senα = Senβ.Senα e QC=Senβ.Cosα.
Olhando agora para o triângulo OPC, temos:
Sen(α+β)= PC/1 = AB+QC = Senα.Cosβ + Senβ.Cosα
Cos(α+β)= PO/1 = OA-BQ = Cosα.Cosβ - Senα.Senβ
Para a Tangente, dividimos uma pela outra:
Tan(α+β)= Sen(α+β)/Cos(α+β) = Senα.Cosβ + Senβ.Cosα/Cosα.Cosβ - Senα.Senβ (Dividindo em cima e embaixo por Cosα.Cosβ)
Tan(α+β)= tanα+tanβ/1∓ tanα.tanβ
Para as de subtração, escrevemos α-β = α+ (-β) e usamos paridade.
W_Yuri- Padawan
- Mensagens : 67
Data de inscrição : 26/08/2018
Idade : 26
Localização : Muriaé - MG
Re: Demonstração de soma de arcos (Trigonometria)
por Giovana Martins Seg 14 Jan 2019, 20:07
Um outro jeito legalzinho de demonstrar as duas primeiras relações (soma de arcos para o seno e cosseno) é por números complexos.
\\e^{\theta i}=cos(\theta)+isen(\theta)=cis(\theta)\\\\cis(x)cis(y)=e^{xi}e^{yi}=e^{(x+y)i}=cis(x+y)\\\\\left [ cos(x)+isen(x) \right ]\left [ cos(y)+isen(y) \right ]=cis(x+y)\\\\\left [ cos(x)cos(y)-sen(x)sen(y) \right ]+i[sen(x)cos(y)+sen(y)cos(x)]=cis(x+y)\\\\\therefore \ cos(x)cos(y)-sen(x)sen(y)=cos(x+y)\\\\\therefore \ sen(x)cos(y)+sen(y)cos(x)=sen(x+y)
____________________________________________
Charlotte de Witte - Universal Nation
Giovana Martins- Grande Mestre
- Mensagens : 8571
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
W_Yuri gosta desta mensagem
Tópicos semelhantes» Trigonometria - Soma de Arcos
» Trigonometria, soma e subtração de arcos.
» Trigonometria - Soma e Subtração de Arcos
» Demonstração de Arcos.
» Demonstração - Arcos Triplos a nível IME/ITA
» Trigonometria, soma e subtração de arcos.
» Trigonometria - Soma e Subtração de Arcos
» Demonstração de Arcos.
» Demonstração - Arcos Triplos a nível IME/ITA
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
