(Upf 2018)

Tentei resolver, mas não estou conseguindo... Alguém pode me ajudar?

A medida de cada aresta do cubo da figura 1 é 2 cm, e os pontos A, B e C são pontos médios de três arestas. Seccionando o cubo por um plano que passe por ABC, podemos retirar o sólido que se forma em seu vértice. Se repetirmos esse procedimento em todos os vértices do cubo, obtemos um cubo truncado, como mostra a figura 2.

O volume do cubo truncado, em 3 cm , é 


Resposta: 20/3

Os cortes em cada vértice criam uma pirâmide onde a base é um triângulo equilátero.

Os triângulos das faces laterais são retângulos e idênticos

Tomando o triângulo BVC, retângulo em V, temos os lados BV = 1, VC = 1 e BC = √2(utilize o Teorema de Pitágoras).

Como os triângulos são idênticos BC = AB = AC = √2.

Utilize a fórmula que compara o raio da circunferência circunscrita com o lado do triângulo(lembre-se que todo triângulo é circunscritível).

Fazendo isso encontrará R=\frac{\sqrt{2}}{\sqrt{3}}

As arestas laterais são todas iguais a 1.

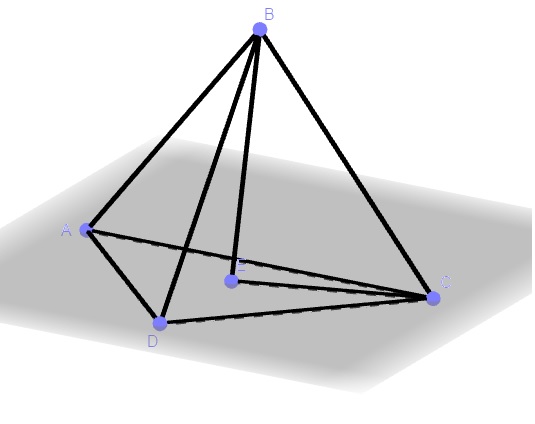
BE é altura da pirâmide
ED é o raio da circunferência circunscrita
BC é aresta lateral

Fazendo Pitágoras, temos:
1^2=h^2+R^2
\\1=h^2+\frac{2}{3}
\\h=\frac{\sqrt{3}}{3}

O volume procurado é o volume do cubo - 8.volume da pirâmide.

Daí:
2^3-8.\frac{1}{3}.\frac{(\sqrt{2})^2.\sqrt{3}}{4}.\frac{\sqrt{3}}{3}
\\8 - \frac{4}{3}
\\\frac{20}{3}

Muitíssimo obrigado

Dá para simplificar.

Cada uma das pirâmides retiradas é reta. Tomando a ABCV como exemplo, seu volume é:
v = (1/3).(AV.BV/2).VC = (1/3).(1*1/2).1 = 1/6 cm^3

O volume do cubo truncado será:
V = 2^3 - 8.v = 8 - 4/3 = 20/3 cm^3