Função quadrada e logaritmo

por eestudo2 Seg 17 Dez 2018, 09:52

Qual a relação entre x e y?

$Função quadrada e logaritmo Gif$
$Função quadrada e logaritmo Gif$
$Função quadrada e logaritmo Gif$
$Função quadrada e logaritmo Gif.latex?d%29%20%5C%2C%20%5C%2C%20%5C%2C%20y%3D0%2C01.10%5E%7Blog%20x%5E%7B2%7D%7D$

Achei a opção A como resposta. Estou correta?

OBS: O gráfico é uma parábola, desculpem-me o gráfico péssimo... não tenho a foto do exercício e nem o gabarito

por **Giovana Martins** Seg 17 Dez 2018, 10:41

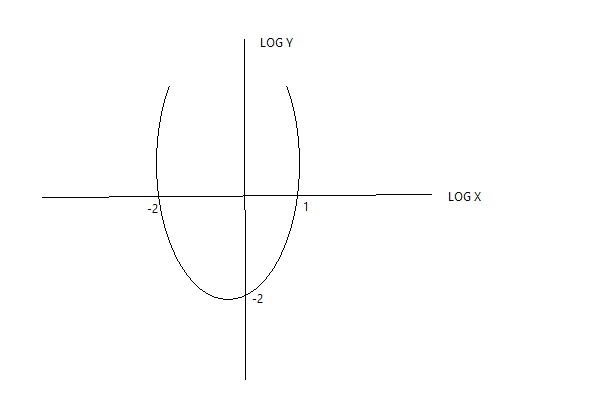
Seu gráfico ficou engraçado hahahaha

O que você pode fazer é o seguinte: pegue um par ordenado conhecido do gráfico e jogue em cada uma das funções fornecidas. Se houver coerência no resultado encontrado, pronto, você achou a alternativa certa. Peguemos o ponto (1,0). Esse é o melhor ponto pois sabemos que o logaritmo decimal de 1 é igual a zero.

\\(1,0)\to 0=0,01.(1)^3\to 0\neq 0,01\\\\(1,0)\to 0=(1)^2+1-2\to 0=0\ \text {(ok)}\\\\(1,0)\to 0=(1)^2+1+2\to 0\neq 4\\\\(1,0)\to 0=0,01.10^{log(1)^2}.1\to 0\neq 0,01\\\\\therefore\ \boxed {y=x^2+x-2}

por eestudo2 Seg 17 Dez 2018, 11:05

Tive que dar uma improvisada no desenho hehehe

Muito obrigada pela ajuda

Me ajudou muito!! Smile

por **Giovana Martins** Seg 17 Dez 2018, 11:07

Disponha

!

por **Elcioschin** Seg 17 Dez 2018, 11:26

Achando a solução diretamente

y = a.x² + b.x + c

Para x = 0 ---> y = - 2 ---> c = - 2

Para x = 1 ---> y = 0 ---> a + b - 2 = 0 ---> *2 ---> 2.a + 2.b = 4 ---> I

Para x = - 2 ---> y = 0 ---> 0 = 4.a - 2.b - 2 ---> $a - 2.b = 2 ---> II

I + II ---> 6.a = 6 ---> a = 1 ---> b = 1

y = x² + x - 2

por eestudo2 Seg 17 Dez 2018, 14:49

Poderia me dizer o erro em minha conta?

encontrei a=1 e b=1

logy=logx²+logx - 2 eu encontro:
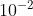
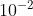
logy = logx²+ log x + log $Função quadrada e logaritmo Gif$
log y = log x².x. $Função quadrada e logaritmo Gif$
y=0,01.x³

por **Elcioschin** Seg 17 Dez 2018, 16:20

O logaritmo de uma soma NÃO é igual à soma dos logaritmos

log(a + b) ≠ loga + logb

O correto é log(a.b) = loga + logb

por **Leo Consoli** Seg 17 Dez 2018, 17:09

Acho que vi o erro na resolução por logaritmos, como logx é a variável no lugar de logx^2 deveria ser (logx)^2, ai seria algo assim:
logy=(logx)^2 + logx - 2