Um tanque com formato de cilindro circular reto contém

Um tanque com formato de cilindro circular reto contém combustível na altura x metros, conforme mostra a figura. Usando todo o volume armazenado, é possível encher completamente, sem sobras, m reservatórios de mesmo formato cilíndrico, de volume igual a 3 m3 cada, ou então n reservatórios de mesmo formato cilíndrico, de volume igual a 4 m3 , sendo m e n números inteiros positivos, com m + n ≤ 12.

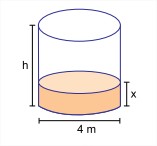
Usando a aproximação π = 3 e sabendo que x=h/5, é correto afirmar que a altura aproximada desse tanque, indicada por h na figura, é 
(A) 5 m. (B) 8 m. (C) 5,5 m. (D) 6,5 m. (E) 6 m.
resposta A

d = 4 ---> r = 2

Possibilidades para m, n ---> 12.1, 6.2, 4.3 ---> m > n

pi.r².x = 3.m ---> 3.2².x = 3.m ---> m = 4.x ---> I
pi.2².x = 4.n ---> 3.2².x = 4.n ----> n = 3.x ----> II

I : II ---> m/n = 4/3 ---> m = 4 e n = 3

I ---> 3.2².x = 3.4 --> x = 1

x = h/5 ---> h = 5.x ---> h = 5 m

Elcioschin escreveu:d = 4 ---> r = 2

Possibilidades para m, n ---> 12.1, 6.2, 4.3 ---> m > n

pi.r².x = 3.m ---> 3.2².x = 3.m ---> m = 4.x ---> I
pi.2².x = 4.n ---> 3.2².x = 4.n ----> n = 3.x ----> II

I : II ---> m/n = 4/3 ---> m = 4 e n = 3

I ---> 3.2².x = 3.4 --> x = 1

x = h/5 ---> h = 5.x ---> h = 5 m

Não entendi as a passagens pi.r².x = 3.m  e pi.2².x = 4.n.
Meu raciocínio foi o seguinte:
#(pi.r².x)/3=m  ou seja o volume armazenado dividido pelo volume de do novo reservatório(a) dará m reservatórios.
#(pi.r².x)/4=n  ou seja o volume armazenado dividido pelo volume de do novo reservatório(b) dará n reservatórios.

pow...

Seu raciocínio é a tradução do que já foi dito no enunciado. O que interessa é achar o valor de x, para obtermos a altura h. Para isto necessitamos saber quanto é m ou n.

Vou exibir a solução do Élcio de uma outra forma; talvez fique mais claro.

Medeiros escreveu:pow...

Seu raciocínio é a tradução do que já foi dito no enunciado. O que interessa é achar o valor de x, para obtermos a altura h. Para isto necessitamos saber quanto é m ou n.

Vou exibir a solução do Élcio de uma outra forma; talvez fique mais claro.

Entendi sua resolução,mas queria saaber pq a minha dá errado.
Chego em 4x=m  e 3x=n.         
dado  m+n ≤ 12 e x=h/5
4x+3x≤12
7x≤12
7h/5≤12
h=60/7

Pode me explicar??

A resolução NÃO é minha, apenas reescrevi a do Élcio.

A sua resolução permite descobrir apenas que h é menor ou igual a 60/7 (você não pode burlar aquele sinal de desigualdade), e isto é verdade mas não é suficiente porque não chega ao valor exato de h.

É peciso calcular os valores de m e n, individualmente, usando as dicas do enunciado:
m e n são inteiros e positivos -- observe que não podem ser zero;
m + n <= 12

Por isso que o Élcio obteve aquela proporção: m/n = 4/3
poderia ser:
m = {4, 8, 12, 16,...} e
n = {3, 6, 9, 12, ...}
mas somente os primeiros elementos satisfazem m+n<=12. Logo m=4 e n=3.