Posição relativa das retas.

Considere as retas: r:{ x=  t      t  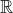   e s:{ x= 1+ks       s      
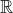
                                 y= 1-t                      y= s
                                 z= 2t                       z= 2+2ks

Determine, caso exista, os valores de k 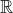 , tais que as retas r e l sejam:

a) coincidentes
b) paralelas e não coincidentes
c) concorrentes
d) reversas
e) Em quais dos casos anteriores as duas retas determinam um único plano?
    Escreva as equações paramétricas de tais planos em cada caso.

(a) Para determinar os valores de k para que as retas r e l sejam coincidentes as três equações do sistema abaixo precisam ser verificadas para todos os valores reais de t e s:  
t = 1 + ks
1 − t = s 
2t = 2 + 2ks ⇐ ⇒ ( t = 1 + ks 
                           1 − t = s 
A equivalência acima é verdadeira, pois a terceira equação o é o dobro da primeira. 
Substituindo o valor de s da segunda equação, na primeira equação temos t − 1 = k(1 − t), como essa igualdade tem que valer para todo t ∈ R, temos que k = −1. 

 (b) A reta r é a reta que passa pelo ponto P = (0, 1, 0) e paralela ao vetor v = (1, −1, 2). 
Para que as retas r e l sejam paralelas o vetor direção de l tem que ser paralelo ao vetor direção de r,ou seja, deve existir um λ ∈ R tal que (1, −1, 2) = λ(k, 1, 2k) ⇐ ⇒ k = λ = −1. 
Vimos no item anterior que se k = −1 as retas são coincidentes, portanto não existe k ∈ R que torne as retas r e l paralelas e não coincidentes.

 (c) Queremos condições sobre k para que as retas r e l sejam concorrentes. Elas não podem ser coincidentes, isto é , k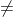  −1 mas, devem ter um ponto em comum. Para encontrar tal ponto, vamos resolver o sistema:  t = 1 + ks 
                            1 − t = s 
                            2t = 2 + 2ks ⇐⇒  t = 1 + ks 
                                                     1 − t = s . 
Substituindo o valor de s da segunda equação na primeira equação temos t − 1 = k(1 − t) ⇐⇒ (t − 1) − k(1 − t) = 0 ⇐⇒ (t − 1)(k + 1) = 0 como k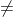  −1, entãoo t − 1 = 0, isto é, t = 1. 
Substituindo o valor t = 1 na segunda equação temos que s = 0. 
Fazendo t = 1 na equação de r e s = 0 na equação de l temos que o ponto (1, 0, 2) ∈ r ∩ l.
 Portanto, sempre k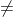  −1 as retas são concorrentes. 

(d) Vimos nos itens anteriores que as retas r e l são coincidentes de k = −1 e são concorrentes se
 k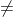 −1. Logo não existe k ∈ R tais que as retas r e l sejam reversas.


 (e) Como as retas são coincidentes ou concorrentes, só determinarão um único plano quando forem concorrentes (item (c)). Observe que as retas r e l são paralelas, respectivamente, aos vetores 
(1, −1, 2) e (k, 1, 2k) e que o ponto (1, 0, 2) ∈ r ∩ l. Portanto o plano procurado é
 (x, y, z) = (1, 0, 2) + (1, −1, 2)t + (k, 1, 2k)s, t, s ∈ R. 
As equações paramétricas do plano Πk, k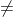  −1 são:
 Πk : x = 1 + t + ks 
y = −t + s 
z = 2 + 2t + 2ks              t e s ∈ R.