Cone circular reto

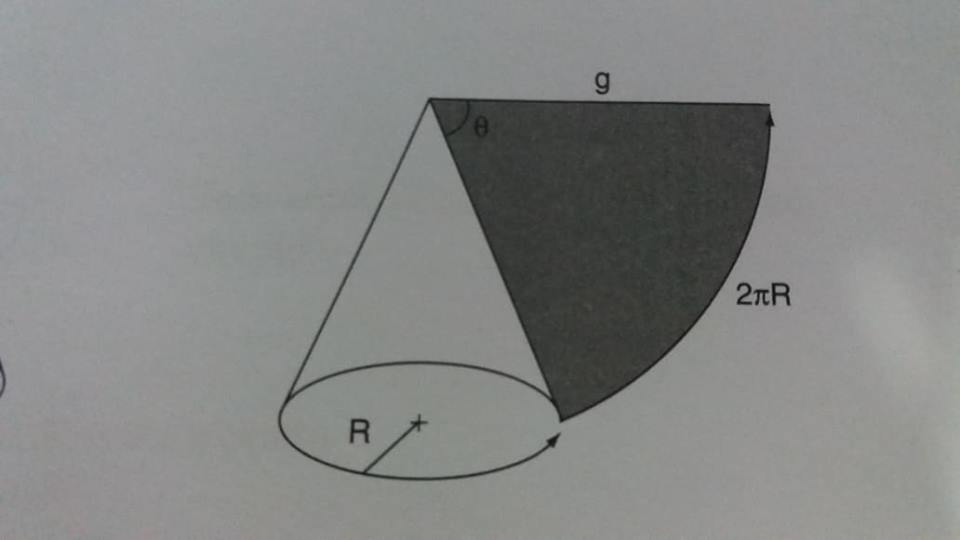
Um chapeuzinho, distribuído em uma festa, tem a forma de um cone circular reto e, quando planificado, fornece um semicírculo com 10 cm de raio. Para o cone, que representa o formato de um chapeuzinho:

a) o raio da base é 10 cm.

b) a área da base é 50∏ cm².

c) a área lateral é 25∏ cm².

d) a geratriz mede 5 cm.

e) o volume é (125∏√3)/3 cm³.

Eu consigo enxergar a planificação, e consigo enxergar que a geratriz vale 10 cm. Mas não consigo achar o raio da base do cone para calcular as outras alternativas...
Sempre faço essa planificação, em vermelho, que dá pra eu visualizar bem:


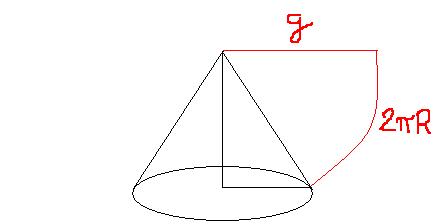
Alguém pode me ajudar, por favor??

Seu desenho tem um erro: co correto é pi.R (e não 2.pi.R) porque é um semicírculo

Sendo r o raio da base do cone (é o raio menor mostrado na sua figura), o perímetro da base do cone vale 2.pi.r

R = 10 ---> g = 10

2.pi.r = pi.R ---> 2.r = 10 ---> r = 5 

h² = g² - r² ---> h² = 10² - 5² ---> h² = 75 ---> h = 5.√3

V = (1/3).pi.r².h ---> V = (1/3).pi.5².(5.√3) ---> V = 125.pi.√3/3 cm³

Elcioschin escreveu:Seu desenho tem um erro: co correto é pi.R (e não 2.pi.R) porque é um semicírculo

Élcio, não entendi essa parte...
Minha apostila traz assim:



Pensei que fosse 2piR justamente por ser a planificação da circunferência que fica na base do cone...

O desenho acima não está coerente com a minha solução e a do Medeiros: nós chamamos de R o raio do semicírculo e r o raio do cone. No seu desenho R aparece como raio do cone. O seu desenho então deve ser mudado para r, para você acompanhar nossa solução.

Desenhe um semi-círculo de raio R = 10 cm. O comprimento do arco do semicírculo vale pi.R = 10.pi
Dobrando-se este semi-círculo, constrói-se um cone, com as seguintes características:

1) O raio R do semi-círculo é a própria geratriz do cone: g = R ---> g = 10
2) O comprimento do arco do semicírculo (10.pi) é igual ao perímetro da circunferência da base do cone: 2.pi.r = 10.pi

Com isto temos r = 5 cm

3) Use Pitágoras e calcule a altura do cone: h² = g² - r²
4) Calcule o volume do cone