Trigonometria - EFOMM/2009

por Oziel Qui 12 Jul 2018, 17:42

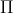A equação $Trigonometria - EFOMM/2009 Gif$ = 0 tem quantas raízes no intervalo [0;2 $Trigonometria - EFOMM/2009 Gif$ ] ?

a) zero

b) uma

c) duas

d) três

e) quatro

obs: não tenho o gabarito

por **Giovana Martins** Qui 12 Jul 2018, 17:50

Essa equação não tem solução analítica. Você tem que fazer o seguinte:

2^-x=-cos(∏-x) → 2^-x=cos(x)

Faça f(x)=2^-x e g(x)=cos(x). Esboce os gráficos de f(x) e g(x) no intervalo pedido. O número de intersecções entre os gráficos de f(x) e g(x) será o número de soluções.

Spoiler:

por **Matheus Tsilva** Qui 12 Jul 2018, 18:55

Olá ,
Muito bom Giovana , ótima ideia.
Eu tentei fazer de um jeito diferente , mas precisamos das alternativas.
Utilizando o teorema de Bolzano , que nos diz que num intervalo ]a,b[ , para uma equação polinomial , P(a) e P(b) tenham os mesmos sinais , no intervalo dado terá um número par de raízes , caso seja de sinais opostos , teremos um número ímpar de raizes.

Observamos que 0 é solução da equação , por uma pequena inspeção.
2pi já não é solução.

Vamos analisar por teorema de Bolzano , o intervalo ]1,2pi[ , temos que o número de raízes no intervalo é par , podendo ser 0 ou 2 (únicas condições para acharmos uma resposta)

Agora consideramos entre ]pi,2pi[ , temos que o número de raízes é ímpar sendo então 1 ou 3 ( para haver resposta)

Como ]pi,2pi[ está contido em ]1,2pi[ , o número de raízes nesse intervalo não pode ser 0 , logo pelas condições colocadas só pode ser 2 raízes

Fazendo um último Bolzano entre ]-1,2pi[ , temos que há um número ímpar de raízes , logo só podemos ter a resposta de 3 raízes.

Cartiação é uma arte.