Triângulo inscrito na circunferência

por Pedro29 Dom 27 maio 2018, 20:27

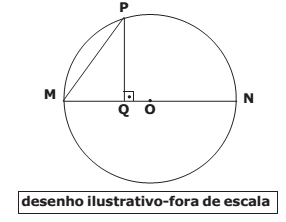
Na figura , o raio da circunferência de centro O é $Triângulo inscrito na circunferência Mimetex_$ e a corda $Triângulo inscrito na circunferência Mimetex_$ mede $Triângulo inscrito na circunferência Mimetex_$ . A medida, em centímetros, do segmento $Triângulo inscrito na circunferência Mimetex_$ é

a) $Triângulo inscrito na circunferência Mimetex_$

b) $Triângulo inscrito na circunferência Mimetex_$

c) $Triângulo inscrito na circunferência Mimetex_$

d) $Triângulo inscrito na circunferência Mimetex_$

e) $Triângulo inscrito na circunferência Mimetex_$ <- GABARITO

Amigos, eu usei a formula de Heron no triangulo isósceles

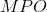Triângulo inscrito na circunferência Codeco14

com base

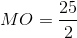Triângulo inscrito na circunferência Codeco15

e catetos

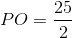Triângulo inscrito na circunferência Codeco13

e

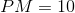Triângulo inscrito na circunferência Codeco12

de altura

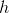Triângulo inscrito na circunferência Codeco16

(que seria o $Triângulo inscrito na circunferência Mimetex_$ pedido na questão) para calculo da área do mesmo. Feito isso, eu igualei a formula da área do triangulo, porém, chego na resposta de

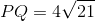Triângulo inscrito na circunferência Codeco11

. Observem.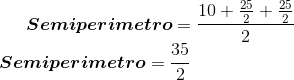

Triângulo inscrito na circunferência Codeco18

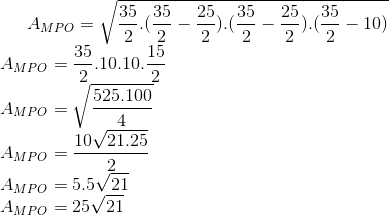
Triângulo inscrito na circunferência Codeco17

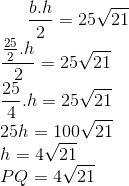
Alguém, por favor, me diga onde que errei? Pois to achando que errei por um detalhe pequeno já que se aproximou bastante do gabarito...

Me desculpem pelas letras grandes no Latex, é a primeira vez que estou usando. Neutral

Grato!

por **Lucas Pedrosa.** Dom 27 maio 2018, 20:45

Pedro, posso sugerir outro modo de fazê-la?

Traçando o segmento NP, será formado um triângulo NMP retângulo em P.

Os triângulos NMP e MPQ são semelhantes.

MP/MN = PQ/PN

MN² = MP² + PN² --> PN = 5√21

MP/MN = PQ/PN --> 10/25 =PQ/5√21 --> PQ = 2√21

por **Lucas Pedrosa.** Dom 27 maio 2018, 20:50

Ah, e o seu erro foi no cálculo da área. A área é igual a (25√21)/2.

por Pedro29 Dom 27 maio 2018, 21:01

Oi Lucas, esse outro método de fazer eu vi, mas fiquei curioso quanto a esse outro método que é o que estou propondo.

Nao entendi por que a área foi dividida por 2...poderia me explicar, por gentileza?

Por que no calculo a raiz de 4 vira 2 e logo depois o 2 corta com o 10 de cima...

por **Lucas Pedrosa.** Dom 27 maio 2018, 21:11

\\\sqrt{(\frac{35}{2})\cdot (\frac{35}{2}-\frac{25}{2})\cdot (\frac{35}{2}-\frac{25}{2})\cdot (\frac{35}{2}-10)}\\\\=\sqrt{\frac{35}{2}\cdot \frac{10}{2}\cdot \frac{10}{2}\cdot \frac{15}{2}}=\sqrt{\frac{7\cdot 5\cdot 10\cdot 10\cdot 5\cdot 3}{2^{4}}}=\frac{50\sqrt{21}}{4}=\frac{25\sqrt{21}}{2}