Distância entre retas

por Cristina Lins Sex 09 Fev 2018, 14:36

Considere as retas r: x = 1 + t, y = -2 + 3t, z = 4 - t, t pertencente a R, e s: x = 2k, y = 3 + k , z = -3 + 4k, k pertencente a R. A distância entre elas é dada por:

a) 51/191^1/2

b) 17/230^1/2

c) 13/230^1/2

d) 13/ 191^1/2

e) 8/230^1/2

por Caio Fernandes Seg 12 Fev 2018, 11:13

(1º) Considere uma terceira reta "m", perpendicular simultaneamente as retas "r" e "s".
(2º) Marque o ponto de intersecção da reta "m" com a reta "r", podemos chamar este ponto de ponto A $(x_{r},y_{r},z_{r})$ ---> A(1+t, -2+3t, 4-t)
(3º) Marque o ponto de intersecção da reta "m" com a reta "s", podemos chamar este ponto de ponto B $(x_{s},y_{s},z_{s})$ ---> B(2k, 3+k, -3+4k)

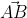
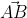Observe que a distância entre o ponto A e o ponto B é a distância entre as retas "r" e "s", logo basta acharmos o módulo do vetor $\vec{AB}$

$\vec{AB}$ = B - A
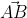$\vec{AB}$ (2k-1-t, k-3t+5, 4k+t-7)

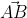| $\vec{AB}$ | = $\sqrt{(2k-1-t)^{2}+(k-3t+5)^{2}+(4k+t-7)^{2}}$

Para acharmos os valores de "t" e "k" podemos nos lembrar que o vetor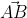 $\vec{AB}$ é perpendicular as retas "r" e "s", logo também será perpendicular ao vetores diretores das respectivas retas. Então, $\vec{AB}\cdot \vec{v_{r}}$ = 0 e $\vec{AB}\cdot \vec{v_{s}}$ = 0 (produto escalar)

vetor diretor da reta r ---> $\vec{v_{r}}$ (1, 3, -1)

vetor diretor da reta s ---> $\vec{v_{s}}$ (2,1,4)

$\vec{AB}\cdot \vec{v_{r}} = 0$
$\vec{AB}\cdot \vec{v_{r}}$ = (2k-1-t).1 + (k-3t+5).3 + (4k+t-7).(-1) = 0

$\vec{AB}\cdot \vec{v_{s}}$ = 0
$\vec{AB}\cdot \vec{v_{s}}$ = (2k-1-t).2 + (k-3t+5).1 + (4k+t-7).4 = 0

Após resolver o sistema basta, substituir os valores de "t" e "k" na equação |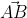 $\vec{AB}$ | = $\sqrt{(2k-1-t)^{2}+(k-3t+5)^{2}+(4k+t-7)^{2}}$