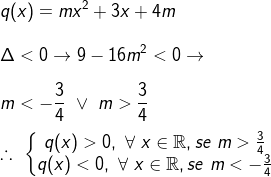Inequação

por **Lucas Pedrosa.** Qua 31 Jan 2018, 23:58

Determine m para que se tenha \forall \;x\in \mathbb{R}:

\\\frac{x}{x^{2}+4}>\frac{x+m}{x^{2}+1}

Resposta: m <-3/4

por **Elcioschin** Qui 01 Fev 2018, 00:13

Leve a fração do 2º membro para o 1º membro

Faça a subtração das frações, usando o mmc (x² + r).(x² + 1) e simplique o numerador

Calcule as raízes do novo numerador. O denominador é sempre positivo.
Logo, o sinal do 1º membro depende apenas do sinal da função do numerador (uma parábola)

por **Giovana Martins** Qui 01 Fev 2018, 00:44

Os fatores f(x)=x²+1 e g(x)=x²+4 são positivos para todo x pertencente aos reais (∆ < 0). Agora, analisemos o numerador:

Élcio, estou com uma dúvida. Quando eu fiz ∆ < 0, posteriormente eu obteria um intervalo de valores para m para os quais q(x) seria maior que zero ou menor que zero para todo x pertencente aos reais, porém, se eu tomar m=1, q(x) não será maior que zero para todo x pertencente aos reais, pelo contrário, neste caso teremos uma parábola com concavidade voltada para cima e que corta o eixo x em x=-4 e x=1. Não tem algo errado nisso?

Nota: m > 3/4 não convém, pois ela leva a uma contradição, já que teoricamente teríamos o numerador positivo para todo x e, consequentemente, a divisão resultaria em um valor positivo, o que contraria a desigualdade da primeira linha da resolução.

por **Giovana Martins** Qui 01 Fev 2018, 00:46

Fiz uma edição.

por **Elcioschin** Qui 01 Fev 2018, 10:48

Giovana

Resumindo o que você fez:

Para termos m.x² + 3.x + 4.m < 0 a parábola deve ter concavidade voltada para baixo (m < 0) e deverá estar abaixo do eixo x, isto é, as raízes devem ser complexas (∆ < 0):

∆ = 3² - 4.m.(4.m) ---> ∆ = 9 - 16.m² ---> 9 - 16.m² < 0 ---> m > 3/4 (não serve, pois m não pode ser positivo) ou m < -3/4

Sua análise está corretíssima.

por **Lucas Pedrosa.** Qui 01 Fev 2018, 11:31

Obrigado!

por **Giovana Martins** Qui 01 Fev 2018, 13:02

Giovana Martins escreveu:

Os fatores f(x)=x²+1 e g(x)=x²+4 são positivos para todo x pertencente aos reais (∆ < 0). Agora, analisemos o numerador:

Élcio, estou com uma dúvida. Quando eu fiz ∆ < 0, posteriormente eu obteria um intervalo de valores para m para os quais q(x) seria maior que zero ou menor que zero para todo x pertencente aos reais, porém, se eu tomar m=1, q(x) não será maior que zero para todo x pertencente aos reais, pelo contrário, neste caso teremos uma parábola com concavidade voltada para cima e que corta o eixo x em x=-4 e x=1. Não tem algo errado nisso?

Nota: m > 3/4 não convém, pois ela leva a uma contradição, já que teoricamente teríamos o numerador positivo para todo x e, consequentemente, a divisão resultaria em um valor positivo, o que contraria a desigualdade da primeira linha da resolução.

Esquece. Estava errando continha Razz

. Obrigada, Élcio.