(Uerj 2011 Específica) Funções Polinomiais

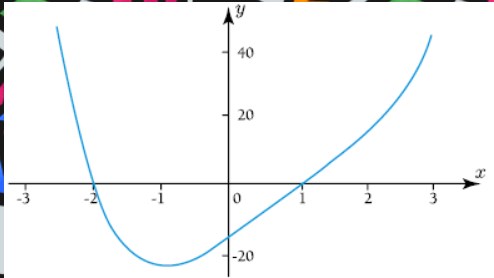
O gráfico acima representa uma função polinomial P de variável real, que possui duas raízes inteiras e é definida por:
P(x) = x⁴ - 3x³ + 2x² + 16x + m

Determine o valor constante representada por m e as quatro raízes desse polinômio.

O que significa 16x m ? Seria 16.x + m? Ou seria 16.x - m ?

Obviamente x = -2 e x = 1 são duas raízes reais (as outras duas são complexas)

http://www.revista.vestibular.uerj.br/questao/questao-discursiva.php?seq_questao=711

"Observando o gráfico da função polinomial, nota-se que -2 também é uma raiz de P. Para determinar as outras duas raízes, deve-se dividir P por (x-1)(x+2), obtendo o polinômio quadrático x2-4x+8. Resolvendo a equação"

Todo polinômio deste tipo pode ser fatorado segundo suas raízes (no caso r, s, t, u)

P(x) = (x - r).(x - s).(x - t).(x - u)

Já sabemos que r = 1 e s = - 2 ---> P(x) = (x - 1).(x + 2).(x - t).(x - u) ---> P(x) = (x² + x - 2).[x² - (t + u).x + t.u]

Mas Élcio, como ele obteve o polinômio quadrático x² - 4x + 8?

Mas esta informação já consta da seu própria mensagem:

Para determinar as outras duas raízes, deve-se dividir P por (x-1)(x+2), obtendo o polinômio quadrático x2-4x+8

Você cometeu um erro de transcrição. A equação correa é essa:

P(x) = x^4 - 3x³ + 2x²+ 16x + m

Como o mestre bem colocou, 1 e - 2 são raízes desse polinômio, logo: (x - 1)(x + 2) = x² + x - 2 divide P(x)

  x^4 - 3x³ + 2x² + 16x + m   |_x² + x - 2 _
- x^4 - x³ + 2x²                          x² - 4x
  - 4x³ + 4x² + 16x + m
 + 4x³ + 4x² - 8x
    8x² + 8x + m

x² + x - 2 divide P(x), se, e somente se, x² + x - 2 divide 8x² + 8x + m

8x² + 8x + m ≡ (x² + x - 2) . Q(x)

Considdere que o símbolo ≡ denota  identidade de polinômios. 

Como estamos dividindo polinômios de mesmo grau, o quociente Q(x) só pode ser uma constante, e como em uma divisão o quociente é único, temos que cada monômio do divisor deve ser identico a cada monômio do dividendo. Logo Q(x) só pode ser 8

8x² + 8x + m = 8x² + 8x - 16

Portanto m = - 16

O simbolo ≡ existe na tabela ao lado SÍMBOLOS ÚTEIS

Perfeito. Editado

Da próxima vez coloque tamanho 13 na fonte do símbolo: ≡ (ao invés de ≡)