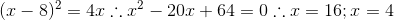Parábola e Trângulo
2 participantes
Página 1 de 1
 Parábola e Trângulo
Parábola e Trângulo
A parábola de equação y²=4x corta a reta de equação x-y-8=0 nos pontos A e B, e seu foco é o ponto F. Encontre a área do triângulo ABF. 

chiaradia12- Iniciante
- Mensagens : 2
Data de inscrição : 11/09/2017
Idade : 23
Localização : Tremembé, São Paulo, Brasil
 Re: Parábola e Trângulo
Re: Parábola e Trângulo
Primeiro descobrindo os pontos onde a parábola corta a reta. Vamos substituir y=x-8 na equação da parábola:
Para x=16 temos y=16-8-->y=8
Para x=4 temos y=4-8---->y=-4
Portanto temos os pontos A e B, (16,8 ) e (4,-4).
Podemos ver que o vértice da parábola se encontra na origem então se compararmos usando a equação de uma parábola y^2=2px podemos perceber que 2p=4----p=2. P(parâmetro) é a distância entre o foco e a reta diretriz e a metade do parâmetro p/2 é a distância do vértice ao foco então encontramos a coordenada do foco:
p/2=1, portanto F(1,0)
Com os três pontos podemos achar a área fazendo:

Espero ter ajudado!!!
Última edição por RodrigoA.S em Ter 12 Set 2017, 15:53, editado 1 vez(es)

RodrigoA.S- Elite Jedi

- Mensagens : 449
Data de inscrição : 12/07/2017
Idade : 25
Localização : Nova Iguaçu
 Re: Parábola e Trângulo
Re: Parábola e Trângulo
Me ajudou muito, porém o valor do determinante é 84.
chiaradia12- Iniciante
- Mensagens : 2
Data de inscrição : 11/09/2017
Idade : 23
Localização : Tremembé, São Paulo, Brasil
 Re: Parábola e Trângulo
Re: Parábola e Trângulo
É verdade!! Já consertei, me desculpa pelo erro bobo !!chiaradia12 escreveu:Me ajudou muito, porém o valor do determinante é 84.

RodrigoA.S- Elite Jedi

- Mensagens : 449
Data de inscrição : 12/07/2017
Idade : 25
Localização : Nova Iguaçu
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos