ESPCEX 2008 - GEOMETRIA ESPACIAL

por victorpapiro Qui 17 Ago 2017, 16:06

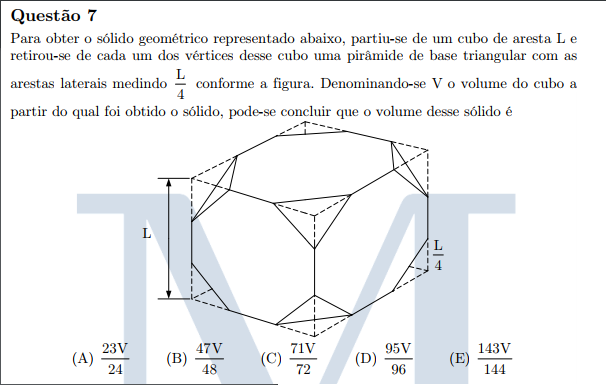
Para obter o sólido geométrico representado abaixo, partiu-se de um cubo de aresta L e retirou-se de cada um dos vértices desse cubo uma pirâmide de base triangular com as arestas laterais medindo L/4, conforme a figura. Denominando-se V o volume do cubo a partir do qual foi obtido o sólido, pode-se concluir que o volume desse sólido é

GAB: B

Rapaziada, boa tarde, eu sei que o volume do sólido = L³ - 8.Vp.

Vp = Volume da pirâmide = Área do triângulo base x Altura da pirâmide/3

Preciso descobrir a altura desta pirâmide ?

por **Elcioschin** Qui 17 Ago 2017, 16:17

Certamente precisa

Desenhe uma das pirâmides com base ABC e vértice V:

1) O vértice V é um dos vértices do cubo
2) AV = BV = CV = L/4
3) Seja O o centro da base ABC ---> OV = h
4) Calcule AB = AC = AD = a ---> a² = (L/4)² + (L/4)²
5) Calcule OA = OB = OC = r (2/3 da altura do triângulo equilátero da base e raio do círculo circunscrito a ele)
5) h² = (L/4)² - r²
6) V = Sb.h/3