ESPCEX 2014 GEOMETRIA ESPACIAL.

por victorpapiro 19/5/2017, 10:06 am

Bom dia galera, alguém consegue essa resolução para mim ? Quebrei a cabeça, porem sem sucesso.

por Faxineiro do ITA 19/5/2017, 10:37 am

victorpapiro escreveu:
Bom dia galera, alguém consegue essa resolução para mim ? Quebrei a cabeça, porem sem sucesso.

Desenha um círculo e um cone inscrito à essa circunferência, temos:
O raio da base do cone é 1. Sabendo que a altura do cone é 4 em seguida só colocar na equação do volume de um cone.

por **Victor011** 19/5/2017, 10:39 am

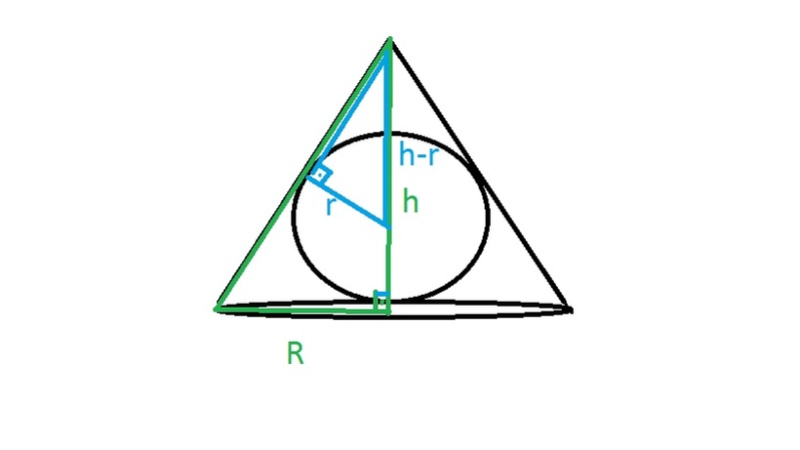
ESPCEX 2014 GEOMETRIA ESPACIAL. Sem_ty12

Pelo desenho acima, basta fazer uma semelhança de triângulos:
Lados do triângulo azul: r, √[(h-r)²-r²] , h-r
Lados do triângulo verde: R, h, √(R²+h²)
semelhança:
\frac{r}{h-r}=\frac{R}{\sqrt{R^2+h^2}}
elevando ao quadrado e passando para o outro lado:
r²(R²+h²)=R²(h-r)²
substituindo os valores de h e r:
R²+16=9R²
R=√2
AREA DO CONE:
S=\frac{1}{3}A\times h
S=\frac{1}{3}\pi R^2\times h
S=\frac{1}{3}2\pi\times 4=\frac{8}{3}\pi cm^3