Heptágono Regular

Tem-se um heptágono regular ABCDEFG; calcular a medida do ângulo que forma a diagonal EG com a bissetriz do ângulo DAG.
a)60º
b)80°
c)70º
d)(310/7)°
e)(270/7)°
R:e

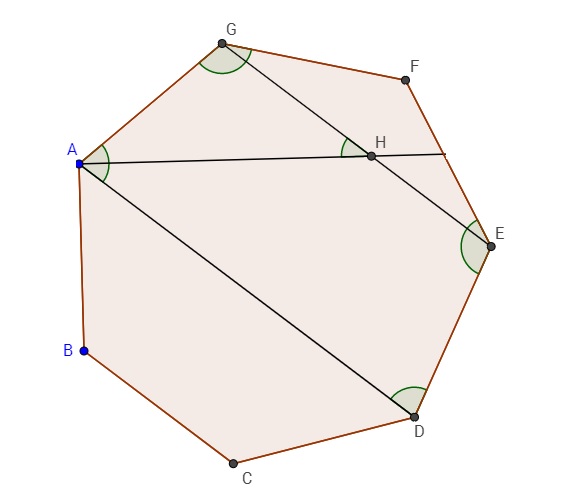
Vamos lá!

Ângulo interno do heptágono: 900/7
Repare que o triângulo EFG é isósceles, pois tem dois lados do heptágono.
Os ângulos internos do triângulo EFG são: 900/7, 180/7, 180/7
O trapézio ABCD é isósceles, pois seus lados não paralelos são lados do heptágono. Logo, seus ângulos internos são 900/7, 900/7, 360/7, 360/7
O ângulo DAG pode ser calculado da seguinte forma: 360/7 + DAG = 900/7 ---> DAG = 540/7
A bissetriz de DAG vai formar dois ângulos de 540/14.
Observando o triângulo AGH, o ângulo interno G pode ser obtido da seguinte forma: 180/7 + G = 900/7 ---> G = 720/7
Ainda no triângulo AGH, podemos calcular o ângulo interno H, procurado no exercício: 
540/14 + 720/7 + H = 180
14H = 14.180 - 540 - 2.720
14H = 14.180 - 3.180 - 2.4.180
14H = 14.180 - 3.180 - 8.180
14H = (14 - 3 - .180
14H = 3.180
H = 3.180/14
H = 270/7