Raio Semicírculo Inscrito
3 participantes
Página 1 de 1
Raio Semicírculo Inscrito
por wacandido Sex 07 Jul 2017, 18:23
Boa noite, alguém poderia me dar uma luz nessa questão ?? Já tentei de tudo e não sai :/
antecipadamente agradeço
Enunciado: Na figura abaixo, AB = 13, BC = 14, AC = 15 e D é o centro da circunferência. Então, o raio r da circunferência é:
a) 2
b) 3
c) 4
d) 5
e) 6
antecipadamente agradeço
Enunciado: Na figura abaixo, AB = 13, BC = 14, AC = 15 e D é o centro da circunferência. Então, o raio r da circunferência é:
a) 2
b) 3
c) 4
d) 5
e) 6
Última edição por wacandido em Sex 07 Jul 2017, 18:49, editado 1 vez(es)
wacandido- Padawan
- Mensagens : 72
Data de inscrição : 02/10/2012
Idade : 43
Localização : Rio de Janeiro - Brasil
Re: Raio Semicírculo Inscrito
por Claudir Sex 07 Jul 2017, 18:37
Leia as regras do fórum, parceiro. O enunciado precisa ser digitado.
____________________________________________
"Death is so terribly final, while life is full of possibilities." - Tyrion Lannister
Claudir- Monitor
- Mensagens : 1938
Data de inscrição : 13/04/2014
Idade : 28
Localização : Gravataí - RS -
Re: Raio Semicírculo Inscrito
por Elcioschin Sex 07 Jul 2017, 20:08
Dicas para começar:
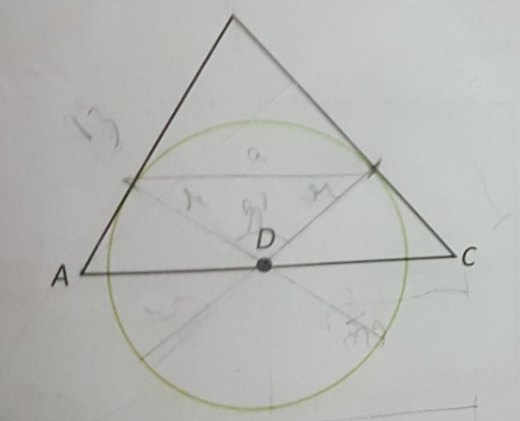
Sejam M e N os pontos de tangência da circunferência com os lados AB e BC
DM = DN = r
Seja BM = BN = b ---> AM = AB - BM ---> AM = 13 - b ---> CN = BC - BN --->
CN = 14 - b
No triângulo retângulo BMD ---> BD² = BM² + DM² ---> BD² = b² + r² --> I
No triângulo retângulo AMD ---> AD² = AM² + DM² ---> AD² = (13 - b)² + r² --->
AD = √[(13 - b)² + r²] ---> II
No triângulo retângulo CND ---> CD² = CN² + BN² ---> CD² = (14 - b)² + r² --->
AD = √[(14 - b)² + r²] ---> III
AD + CD = 15 ---> √[(13 - b)² + r²] = √[(14 - b)² + r²] = 15 ---> III
Tente agora continuar.
Sejam M e N os pontos de tangência da circunferência com os lados AB e BC
DM = DN = r
Seja BM = BN = b ---> AM = AB - BM ---> AM = 13 - b ---> CN = BC - BN --->
CN = 14 - b
No triângulo retângulo BMD ---> BD² = BM² + DM² ---> BD² = b² + r² --> I
No triângulo retângulo AMD ---> AD² = AM² + DM² ---> AD² = (13 - b)² + r² --->
AD = √[(13 - b)² + r²] ---> II
No triângulo retângulo CND ---> CD² = CN² + BN² ---> CD² = (14 - b)² + r² --->
AD = √[(14 - b)² + r²] ---> III
AD + CD = 15 ---> √[(13 - b)² + r²] = √[(14 - b)² + r²] = 15 ---> III
Tente agora continuar.
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tópicos semelhantes» raio do semicírculo inscrito em triângulo
» Decágono inscrito em circunferência de raio 1
» Raio inscrito
» Calcule a medida do raio do círculo inscrito.
» Raio inscrito e circunscrito
» Decágono inscrito em circunferência de raio 1
» Raio inscrito
» Calcule a medida do raio do círculo inscrito.
» Raio inscrito e circunscrito
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
