raio do semicírculo inscrito em triângulo

por **Medeiros** Qua 17 Abr 2024, 23:49

Achei esta questão na internet.

O semicírculo está inscrito no triângulo, o ponto E é de tangência e todos os dados estão no desenho. Qual é a medida do raio do semicírculo?

raio do semicírculo inscrito em triângulo Scree170

Spoiler:

por **Elcioschin** Qui 18 Abr 2024, 10:08

Uma figura para ajudar:

raio do semicírculo inscrito em triângulo Atrise10

por **petras** Seg 22 Abr 2024, 14:39

y = CO
x = AO

[latex]x^2+y^2=14^2 (*)\\ \triangle AEK \sim \triangle BDL \sim \triangle ACO:\\ EK=\frac{4y}{14}:DL=\frac{5y}{14}\\ AK=\frac{4x}{14}:LB=\frac{5x}{14}\\ KL=2x-AL-LB=\frac{19x}{14}\\ DN=DL-EK=\frac{y}{14}\\ r(FM)=\frac{EK+DL}{2}=\frac{9y}{28}(**)\\ \triangle_{(ret)}EDN:\\ (2r)^2=EN^2+DN^2=KL^2+DN^2 \rightarrow (\frac{9y}{14})^2=(\frac{19x}{14})^2+(\frac{y}{14})^2 (***)\\ De (*) e (***) y=\frac{38}{3}\\ \therefore r=9.\frac{38}{28.3}=\boxed{\frac{57}{4}}[/latex]
(Solução:LuisFuentes)

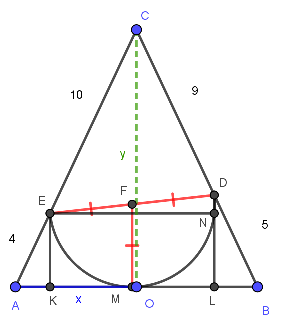
raio do semicírculo inscrito em triângulo Sem_tz17

por irving Seg 22 Abr 2024, 14:57

Ótima resolução, petras.

por **Medeiros** Ter 23 Abr 2024, 00:00

Boa resolução a que você trouxe, Petras. Obrigado pela colaboração.
Hoje já é tarde para mim, outro dia posto uma solução pouco diferente mas não tão enxuta quanto esta.

por **Medeiros** Dom 28 Abr 2024, 22:20

Fiquqei devendo apresentar outra solução e só não o fiz antes por preguiça de escrever. Segue agora e é bem parecida com a do Petras.

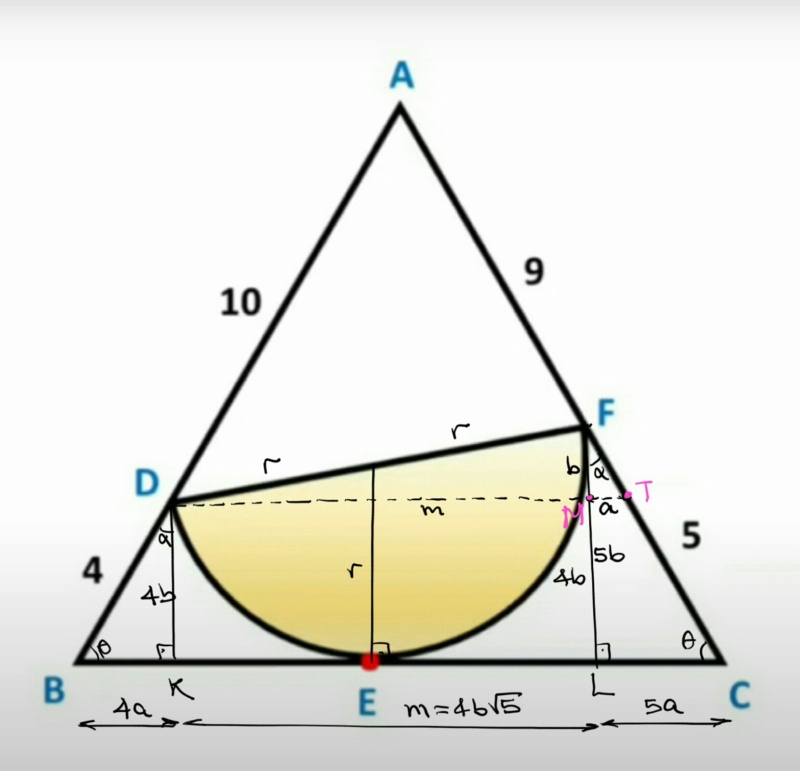
raio do semicírculo inscrito em triângulo Scree252

\( \triangle BAC\ é\ isósceles \)
\( \triangle BKD \sim \triangle CLF \)
[latex]\\ r=\frac{4b+5b}{2}\,\,\rightarrow\,\,r=\frac{9b}{2}\,\,.............(1)[/latex]
\( \triangle DMF:\ DF^{2} = (2r)^{2} = DM^{2}+FM^{2}\ \rightarrow\ 81b^{2}=b^{2}+m^{2}\ \rightarrow\ m=4b\sqrt{5} \)
[latex]\\\triangle ADT \sim \triangle ABC\,\,\rightarrow\,\,\frac{\overset{5}{\cancel{10}}}{\underset{7}{\cancel{14}}}=\frac{4b\sqrt{5}+a}{4b\sqrt{5}+9a}\\\\ 20b\sqrt{5}+45a=28b\sqrt{5}+7a\,\,\rightarrow\,\,{\underset{19}{\cancel{38}}}a={\underset{4}{\cancel{8}}}b\sqrt{5}\,\,\rightarrow\,\,a=\frac{4b\sqrt{5}}{19}\,.........(2)[/latex]

\( Pitágoras\ \triangle BKD:\ (4a)^{2}+(4b)^{2}=4^{2}\ \rightarrow\ a^{2}+b^{2}=1\ .........(3) \)

\( (2)\ em\ (3):\ \left( \frac{4b\sqrt{5}}{19} \right )^{2} + b^{2} = 1\ \rightarrow\ b^{2}=\frac{361}{441}\ \rightarrow\ b=\frac{19}{21}\ .......(4) \)

[latex]\\ \text{(4) em (1):}\,\,\,\,\, r=\frac{{\overset{3}{\cancel{9}}}}{2} \cdot \frac{19}{{\underset{7}{\cancel{21}}}}\,\,\rightarrow\,\,\boxed{\, r=\frac{57}{14}\,}[/latex]

Solução: GeoMathry