Determina dominio função
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Determina dominio função
Determina dominio função
Determine o domínio da função f(x) = sqrt(x² + 7x + 12) + sqrt[(4-x²)/(x+2)]
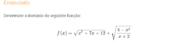
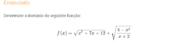
brasileiro1- Jedi

- Mensagens : 395
Data de inscrição : 15/08/2013
Idade : 26
Localização : Rio de Janeiro
 Re: Determina dominio função
Re: Determina dominio função
Lembramos de duas coisas:
- Raiz de número negativo não existe nos conjuntos dos reais.
- Denominador não pode ser zero.
De cara, não pode ser -2 pois zera o denominador na fração.
Também não pode ser um número tal que 4 - x^2 < 0, e não pode ser positivo, pois qualquer valor acima de 2 resulta numa expressão negativa na segunda raiz quadrada.
Por enquanto o domínio é: (-infinito;2]
Em (x² + 7x + 12), temos que as raízes são -3 e -4, e pelo coeficiente de x^2 ser positivo, temos que a concavidade está para cima, o que nos leva a concluir que os valores no intervalo (f(-4);f(-3)) são negativos e não podem ser inclusos na raiz.
Agora temos que o domínio é (-infinito;-4]U[-3;-2)U(-2;2]
Para confirmar nosso resultado, copie e cole "(x^2 + 7x + 12)^(1/2) + [(4-x^2)/(x+2)]^(1/2)" no mecanismo de busca do google e verá que esse é o resultado mesmo.
Espero ter ajudado.
- Raiz de número negativo não existe nos conjuntos dos reais.
- Denominador não pode ser zero.
De cara, não pode ser -2 pois zera o denominador na fração.
Também não pode ser um número tal que 4 - x^2 < 0, e não pode ser positivo, pois qualquer valor acima de 2 resulta numa expressão negativa na segunda raiz quadrada.
Por enquanto o domínio é: (-infinito;2]
Em (x² + 7x + 12), temos que as raízes são -3 e -4, e pelo coeficiente de x^2 ser positivo, temos que a concavidade está para cima, o que nos leva a concluir que os valores no intervalo (f(-4);f(-3)) são negativos e não podem ser inclusos na raiz.
Agora temos que o domínio é (-infinito;-4]U[-3;-2)U(-2;2]
Para confirmar nosso resultado, copie e cole "(x^2 + 7x + 12)^(1/2) + [(4-x^2)/(x+2)]^(1/2)" no mecanismo de busca do google e verá que esse é o resultado mesmo.
Espero ter ajudado.

SergioEngAutomacao- Jedi

- Mensagens : 407
Data de inscrição : 04/06/2017
Idade : 27
Localização : Curitiba
 Tópicos semelhantes
Tópicos semelhantes» Determina dominio função
» [Função] Domínio de uma função de grau 3.
» Domínio da função
» domínio de uma função
» Domínio da função
» [Função] Domínio de uma função de grau 3.
» Domínio da função
» domínio de uma função
» Domínio da função
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












