O uso da regra de cramer em sistemas lineares

Oi a todos,

A regra de cramer é o assunto desse tópico, não sei quando devo usá-la, não sei se devo usá-la, a minha pergunta é, vale a pena usar ela? Por exemplo, é mais rápido usar a substituição de icógnitas nos sistemas lineares ou usar a regra de cramer? No livro dos fundamentos da matemática elementar ele pede pra eu usar cramer aí eu fico na dúvida se uso ou se não uso.

Aguardo a resposta e desde já os agradeço

SE o livro PEDE para usar a Regra de Cramer você tem que usar.

Existem outros modos de resolver sistemas lineares (método da substituição, por exemplo).

Cada caso é um caso: em algumas questões é mais rápido usando Cramer e em outros casos não. Só a experiência vai te ajudar a descobrir o melhor método. importante é você entender e praticar todos eles.

Voçê poderia me dizer se existe alguma desvantagem com o uso dessa regra em algumas ocasiões específicas?

A única desvantagem é o trabalho que dá para usar a Regra de Cramer: Para um sistema de n equações deve-se calcular o valor de n+1 determinantes.

ok, grato !!!

Outro problema do uso da Regra de Cramer é esse.
A Regra de Cramer é uma regra de resolução para sistemas lineares nxn determinados e não deve ser usada como método para discussão de sistemas não homogêneos nxn com n ≥ 3 pois uma determinada impossibilidade pode se apresentar como uma indeterminação aparente como no exemplo do seguinte sistema.



Fazendo primeiro por escalonamento e analisando a característica da matriz completa (Mc) e incompleta (Mi):



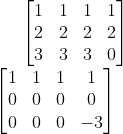
Podemos perceber que a característica da Mc = 2 e da Mi = 1, o que torna o sistema impossível.

Agora vamos analisar o sistema pela Regra de Cramer.
Temos que ∆c = 0, ∆x = 0, ∆y = 0, ∆z = 0
∆c = determinante dos coeficientes
∆x = determinante obtido de ∆c pela substituição da coluna correspondente a incógnita x pelos termos independentes, assim também vale para ∆y e ∆z.
Com isso iremos obter:



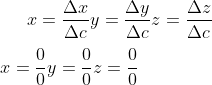
Que nos daria um sistema indeterminado, que não estaria certo, basta comparar a primeira e a terceira equação do sistema.