Geometria Plana - Região Sobreada

por ALDRIN Sáb 02 Abr 2011, 20:17

A figura mostra três circunferências de raios iguais a 4 cm. Calcule o perímetro da região sombreada, se ABCD é um retângulo.

[img]

Geometria Plana - Região Sobreada Figurac

[/img]

(A) 16/3(24∏+2)
(B) 16/3(5∏+9)
(C) 16/3(5∏+7)
(D) 16/3(5∏+2)
(E) 16/3(5∏+3)

por **Adam Zunoeta** Sex 08 Abr 2011, 17:59

A figura em questão é:
Geometria Plana - Região Sobreada Semttulokzf

Vamos achar a área 1, da seguinte forma:
Geometria Plana - Região Sobreada Semttulooa

Então:

Geometria Plana - Região Sobreada 69631893

Geometria Plana - Região Sobreada 53922489

Vamos achar agora a área 3.
Geometria Plana - Região Sobreada 54830861

A área 1 é a mesma que a área 2.
Para a área que falta
Geometria Plana - Região Sobreada 96301517

Pra achar ela eu pensei assim:
Geometria Plana - Região Sobreada 13019023

Porém diverge do gabarito, acho que a idéia é essa. O que vocês acham?

por **JoaoGabriel** Sáb 09 Abr 2011, 08:52

Eu fiz uma conta muito doida quero saber onde eu viajei lol!

Ao meu ver, o modo mais simples de resolver seria calculando cada parte separadamente.

Primeiro, calculemos toda a área colorida FORA dos círculos, ou seja, área do retângulo - área do círculo:

Área do retângulo:

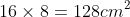
$\\16 \times 8 = 128cm^2$

Área dos círculos:

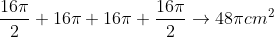
$\\\frac{16\pi}{2} + 16\pi + 16\pi +\frac{16\pi}{2} \to 48\pi cm^2$

Logo a área colorida de fora será:

$\\128 - 48\pi \to 16(8 - 3\pi)$

Veja que é formado no círculo central um hexágono regular de lado = R. Calculemos sua área:

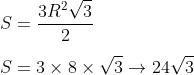
$\\S = \frac {3R^2\sqrt{3}}{2}\\\\S = 3\times 8 \times \sqrt {3 } \to 24\sqrt{3}$

A área colorida no círculo central será a área do círculo - área do hexágono:

$\\16\pi - 24\sqrt{3} \to 8(2\pi - 3\sqrt{3})$

As últimas áreas restantes podem ser calculadas com uma aproximação, ou seja, calcular como se fosse losangos:

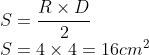
$\\S = \frac {R\times D}{2}\\ S = 4\times 4 = 16 cm^2$

Como tem dois:

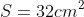
$\\S = 32 cm^2$

Somando tudo:

$\\S_{total} = 16(8 - 3\pi) + 8(2\pi - 3\sqrt {3}) + 32\\S_{total} = 128 - 45\pi + 16\pi - 24\sqrt{3 }+32\\ S_{total} = 160 - 29\pi - 24\sqrt {3}\\ S_{total} = 8(20 - 3\sqrt {3}) - 29\pi$

por ALDRIN Ter 12 Abr 2011, 21:44

Área é diferente de perímetro.

por **adriano tavares** Qui 14 Abr 2011, 00:18

Olá,Aldrin.

O perímetro da região sombreada é igual ao comprimento da circunferência formada pelos arcos AB e CD mais quatro arcos de 120º formados pelas figuras verde e amarela,mais o comprimento da circunferência formada pelos seis setores de 60º , mais duas vezes o comprimento AB e mais quatros vezes o raio que contorna a região amarela .

$8\pi+\frac{32\pi}{3}+8\pi+32+16=16\pi+\frac{32\pi}{3}+48=\frac{16}{3}(5\pi+9)$

Alternativa:B

Eu coloquei a figura em anexo porque não estou conseguindo postar.

Anexos